Vyšetřování průběhu funkce
4. Vykreslení grafu funkce a jeho adaptace
Tradičním úkolem studentů, kteří vyšetřují průběh funkce, je i závěrečné vykreslení jejího grafu. Prokazují tím, že rozumí významu všech údajů, které před tím spočítali, a dovedou je poskládat dohromady. Pro nevidomého je však tento úkol nepoměrně náročnější. Nabízí se tři možné typy adaptace:
- příprava hmatové verze grafu s použitím vhodné asistivní technologie
- textový popis grafu, z něhož bude naprosto zřejmé, jak graf vizuálně vypadá
- výběr z několika již připravených grafů v hmatové podobě
S účastníky workshopu na ICCHP Summer University 2012 v Linci jsme diskutovali výhody a nevýhody všech tří adaptací. Je patrné, že ruční příprava hmatového obrázku funkce je pro nevidomého časově náročná. Navíc úsilí, které musí vynaložit, aby výsledek jeho práce odpovídal skutečnosti, je neporovnatelně větší než u vidících studentů.
Z vlastních zkušeností můžeme potvrdit, že i druhá metoda adaptace není pro nevidomého příliš snadná. Je třeba dlouhodobého tréninku, než se nevidomý student naučí dostatečně srozumitelně popsat graf funkce, jejíž vlastnosti předtím spočítal. Častou chybou je nesprávné pořadí informací, jaké při popisu podává. Soustředí se nejdříve na detaily a až poté charakterizuje obecné vlastnosti. Aby si nevidomý student dokázal výslednou podobu grafu dokonale představit, je třeba výsledný popis spojit s hmatovým obrázkem. Potvrdila to účastnice zmíněného workshopu, učitelka matematiky pro nevidomé: "Myslím si, že pokud nevidomý nemá k dispozici výsledný obrázek a pouze popíše, jak by měla funkce vypadat, o něco přichází. Popis nenahradí stoprocentně obrázek."
Kontrola správnosti popisu grafu může být velmi jednoduchá. Nevidomý student poskytne svůj
popis učiteli či spolužákovi, aniž by mu předem sděli předpis funkce, a požádá jej o nakreslení
grafu. Odpovídá-li nákres požadovanému výsledku, je slovní charakteristika grafu v pořádku.
Tento test jsme udělali i s účastníky několika seminářů pro pedagogické pracovníky.
V jejich průběhu jsme je požádali o zakreslení grafu jen na základě slovního popisu
studenta uvedeného v předchozí části. Potvrdilo se nám, že popis je vytvořen dobře,
informace jsou vhodně strukturované a pro učitele nebyl problém se v nich vyznat.
Zajímavým postřehem může být absence několika detailů, kterých jsme si jako učitelé
nevidomého studenta nevšimli, například absence výpočtu první derivace v inflexním bodě,
který odhalí, jak se graf funkce v okolí zmíněného bodu mění, jak moc přiléhá k ose  .
.
Náročnost úkolu adaptovaného třetí metodou závisí na několika faktorech. Předně, čím více připravených hmatových obrázků, tím je pro nevidomého časově náročnější je porovnat a vybrat z nich ten správný. Další kritérium ovlivňující složitost úkolu spočívá v tom, do jakých detailů se jednotlivé obrázky odlišují. Jsou-li rozdíly nepatrné a ne příliš postřehnutelné, bude pro nevidomého velmi náročné vybrat tu správnou variantu. Myslíme si také, že tato adaptace testuje jiné dovednosti než v případě vidících studentů, kteří nakreslením obrázku potvrdí, že si veškeré vypočítané výsledky umí dát dohromady a představit si je v podobě grafu. Naproti tomu nevidomý si všímá pouze toho, v čem se již připravené hmatové obrázky liší a vybírá ten, který odpovídá výsledkům předchozí práce, tj. vypočítaným vlastnostem funkce.

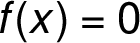 , stanovení,
kdy je graf funkce nad osou či pod osou
, stanovení,
kdy je graf funkce nad osou či pod osou 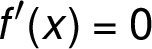 ,
stanovení stacionárních bodů a určení intervalů,
v nichž je funkce
,
stanovení stacionárních bodů a určení intervalů,
v nichž je funkce 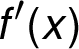 kladná či
záporná
kladná či
záporná 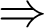 kdy je
kdy je 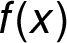 rostoucí či klesající;
určení lokálních extrémů;
rostoucí či klesající;
určení lokálních extrémů;
 ,
stanovení kritických bodů a určení intervalů,
v nichž je je funkce
,
stanovení kritických bodů a určení intervalů,
v nichž je je funkce 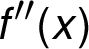 kladná či
záporná
kladná či
záporná  a řešení nevidomého studenta, který vyšetřoval její průběh.
Klíčovou otázkou je adaptace 7. úkolu, tj. vykreslení grafu funkce na základě vypočítaných informací.
Více se tomuto problému věnujeme v části
a řešení nevidomého studenta, který vyšetřoval její průběh.
Klíčovou otázkou je adaptace 7. úkolu, tj. vykreslení grafu funkce na základě vypočítaných informací.
Více se tomuto problému věnujeme v části
 .
.

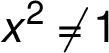
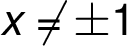

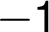 and
and 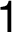 jsou body nespojitosti.
jsou body nespojitosti.













![[-\sqrt{ 3}, \frac{ -3\sqrt{ 3}}{ 2}] [-\sqrt{ 3}, \frac{ -3\sqrt{ 3}}{ 2}]](/amalg/www/images/latex/___lL__d__s_sqrt_L_3_R_,_s_frac_L__d_3_s_sqrt_L_3__norm14_.png)
![[\sqrt{ 3}, \frac{ 3\sqrt{ 3}}{ 2}] [\sqrt{ 3}, \frac{ 3\sqrt{ 3}}{ 2}]](/amalg/www/images/latex/___lL__s_sqrt_L_3_R_,_s_frac_L_3_s_sqrt_L_3_R__R___norm14_.png)

![=\frac{ 2x *(x^2 -1) *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^4} =\frac{ 2x *(x^2 -1) *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^4}](/amalg/www/images/latex/___e__s_frac_L_2x_S__l_x_P_2_d_1_r__S__lL__l_2x_P__norm14_.png)
![=\frac{ 2x *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^3} =\frac{ 2x *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL__l_2x_P_2_d_3_r__S__l_x_P__norm14_.png)
![=\frac{ 2x *[2x^4 -3x^2 -2x^2 +3 -2x^4 +6x^2]}{ (x^2 -1)^3} =\frac{ 2x *[2x^4 -3x^2 -2x^2 +3 -2x^4 +6x^2]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL_2x_P_4_d_3x_P_2_d_2x_P_2_p_norm14_.png)
![=\frac{ 2x *[x^2 +3]}{ (x^2 -1)^3} =\frac{ 2x *[x^2 +3]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL_x_P_2_p_3_rR__R__L__l_x_P__norm14_.png)


 :
:  , A
, A :
:  , V
, V :
:  :
: ![[0, 0] [0, 0]](/amalg/www/images/latex/___lL_0,0_rR____norm14_.png) .
.
 :
:



 .
.
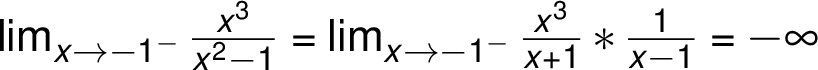



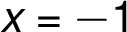 a
a 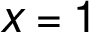 .
.
 .
Graf je omezen asymptotami bez směrnice
.
Graf je omezen asymptotami bez směrnice  je
je
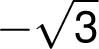 , což je více
než
, což je více
než  , tedy funkční hodnota maxima.
Graf funkce
, tedy funkční hodnota maxima.
Graf funkce 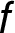 se v intervalu
se v intervalu
 nachází pod asymptotou
nachází pod asymptotou 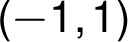 prochází průsečíkem s osami
prochází průsečíkem s osami 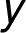 v bodě
v bodě 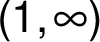 leží
celý nad osou
leží
celý nad osou  je
je 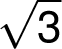 ,
což je méně než
,
což je méně než  ,
tedy funkční hodnota minima.
Graf funkce
,
tedy funkční hodnota minima.
Graf funkce