Ford-Fulkersonův algoritmus
1. Popis standardní metody algoritmu
Ford-Fulkersonův algoritmus slouží k vyhledání maximálního toku
v síti (Síť je orientovaný graf,
kde ohodnocení každé hrany znamená maximální množství energie,
které skrze hranu může procházet).
Pracujeme tedy se sítí 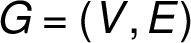 ,
kde
,
kde 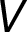 je množina vrcholů včetně zdroje
je množina vrcholů včetně zdroje 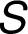 a stoku
a stoku 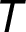 ,
,  je množina orientovaných hran.
Návěští každé hrany zapisujeme ve formátu
je množina orientovaných hran.
Návěští každé hrany zapisujeme ve formátu 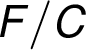 ,
kde
,
kde  značí její kapacitu a
značí její kapacitu a 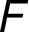 tok,
tj. množství energie, které v ní proudí.
tok,
tj. množství energie, které v ní proudí.
- Na počátku algoritmu nastavíme u všech hran nulový tok.
- Opakovaně hledáme nenasycenou cestu od zdroje ke stoku. Jakmile ji nalezneme, zjistíme minimální rezervu kapacity všech jejích hran, o kterou následně navýšíme tok v síti.
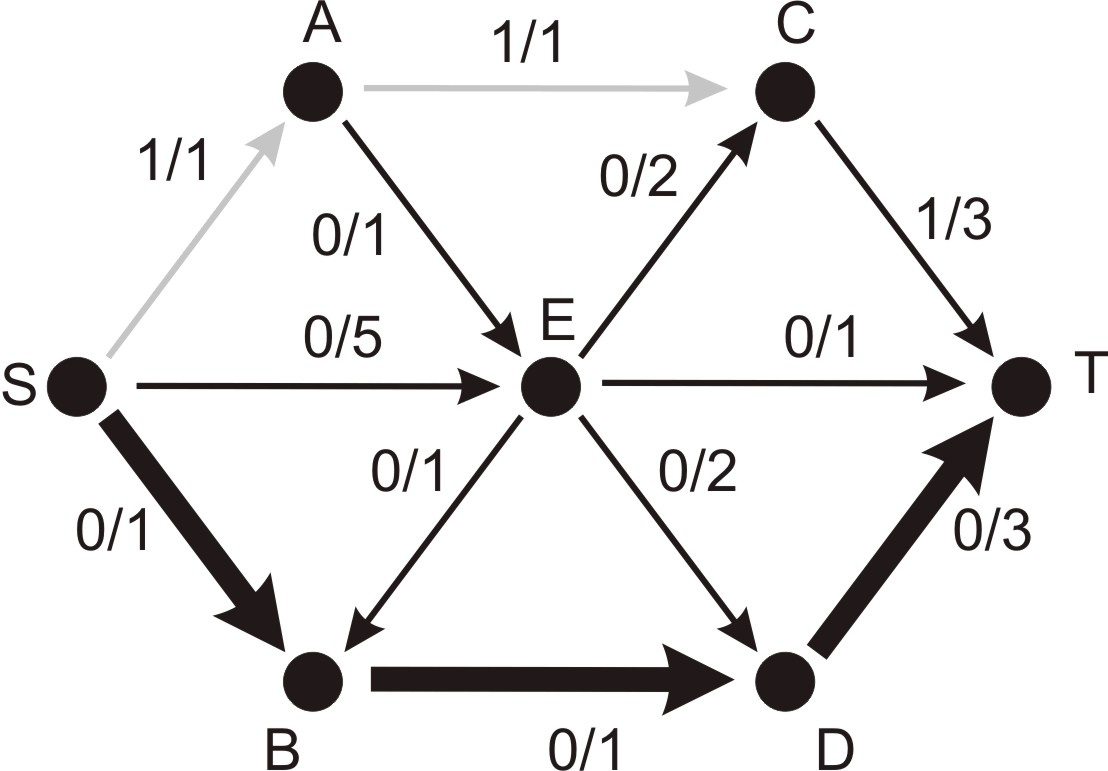
Při běžném provedení algoritmu pracujeme s vizuální reprezentací sítě,
u níž měníme návěští hran. Na Obrázku 1 je
znázorněna síť 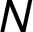 o sedmi
vrcholech s aktuálním tokem 1 (viz cesta
o sedmi
vrcholech s aktuálním tokem 1 (viz cesta 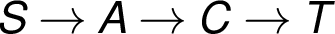 ). Je zvýrazněna
nenasycená cesta
). Je zvýrazněna
nenasycená cesta 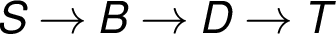 , u níž je minimální rezerva kapacity
hran rovna 1. Můžeme tedy v dalším kroku zvýšit tok v síti a upravit
návěští hran nenasycené cesty, tj. modifikovat
, u níž je minimální rezerva kapacity
hran rovna 1. Můžeme tedy v dalším kroku zvýšit tok v síti a upravit
návěští hran nenasycené cesty, tj. modifikovat 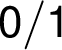 na
na
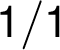 v případě
hran
v případě
hran 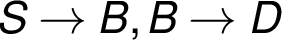 a
a
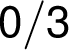 na
na 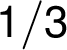 u hrany
u hrany
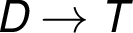 .
.
Pro názornost uvádíme i konkrétní příklad sítě a Animaci 1 naznačující výpočet maximálního toku pomocí Ford-Fulkersonova algoritmu.
Příklad 2: síť 
-
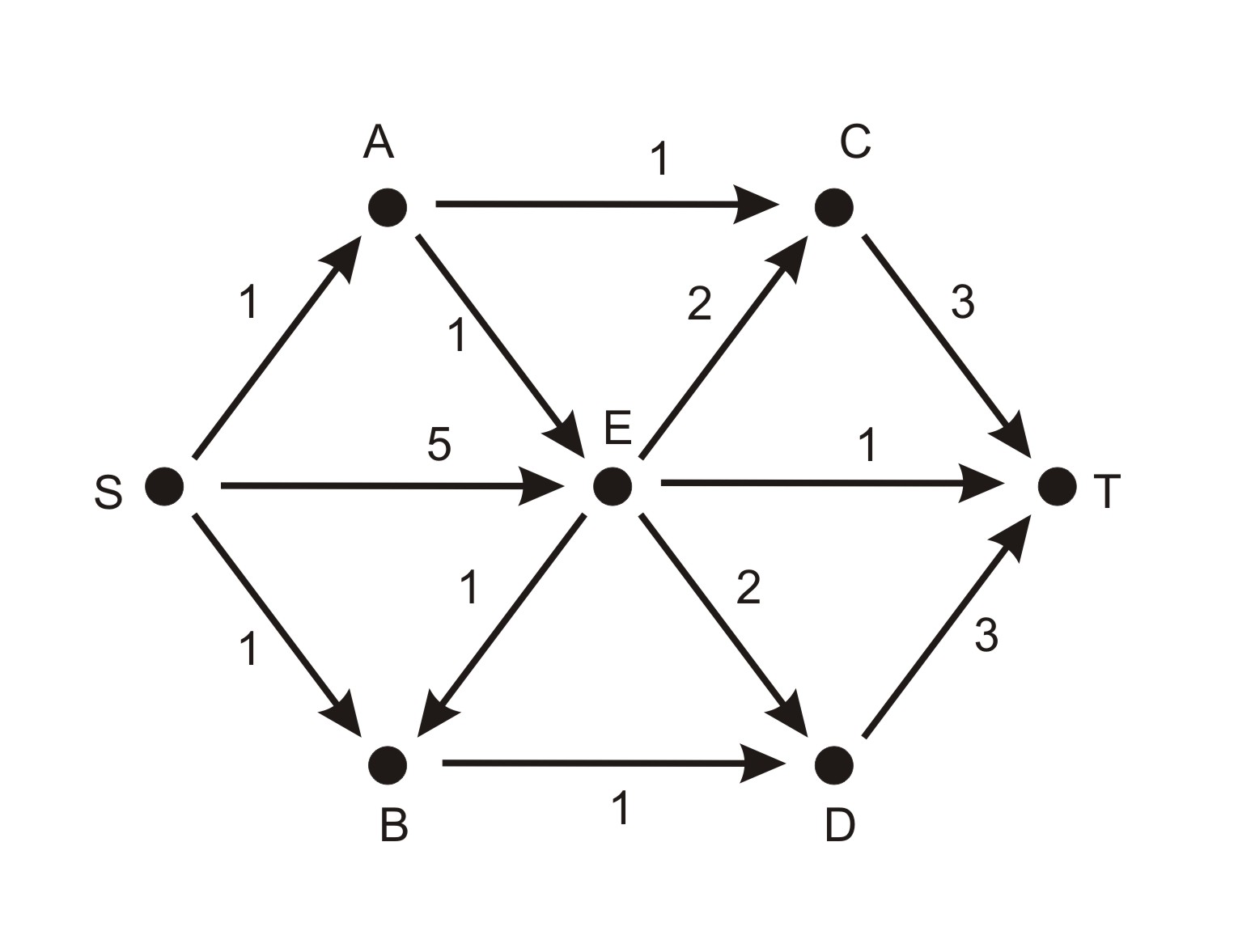
- Počátek algoritmu – síť
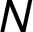 o sedmi uzlech
o sedmi uzlech 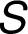 ,
, 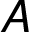 ,
, 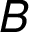 ,
,  ,
,  ,
,  ,
, 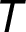
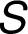 :
: 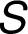 –
–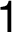 –
–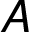
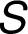 –
–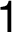 –
–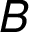
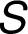 –
–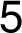 –
–
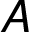 :
: 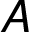 –
–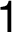 –
–
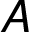 –
–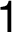 –
–
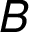 :
: 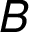 –
–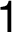 –
–
 :
:  –
–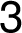 –
–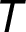
 :
:  –
–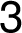 –
–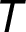
 :
:  –
–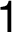 –
–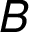
 –
–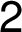 –
–
 –
–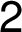 –
–
 –
– –
–
 Nezobrazovat tento popisek
Nezobrazovat tento popisek

 zapisujeme všechny hrany, které začínají v uzlu
zapisujeme všechny hrany, které začínají v uzlu 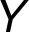 –
–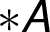 –
–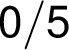
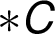 –
–