Kruskalův algoritmus
1. Popis standardní metody algoritmu
Kruskalův algoritmus slouží k vyhledání minimální kostry grafu.
Pracujeme s váženým neorientovaným grafem  ,
kde
,
kde 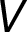 je množina vrcholů,
je množina vrcholů,  je množina neorientovaných hran a
je množina neorientovaných hran a
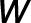 je kladné ohodnocení hran.
je kladné ohodnocení hran.
- Na počátku algoritmu inicializujeme
kostru
 obsahující
všechny vrcholy grafu
obsahující
všechny vrcholy grafu  a prázdnou množinu hran.
a prázdnou množinu hran. - Seřadíme všechny hrany grafu
 vzestupně dle
jejich ohodnocení a v tomto pořadí je postupně zpracováváme.
vzestupně dle
jejich ohodnocení a v tomto pořadí je postupně zpracováváme. - Pokud přidáním konkrétní hrany
 do kostry
do kostry 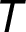 nevniká
kružnice, přidáme
nevniká
kružnice, přidáme  do
do 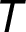 , v opačném případě hranu do
, v opačném případě hranu do 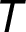 nepřidáme.
nepřidáme. - Po zpracování poslední hrany s nejvyšším ohodnocením získáme minimální kostru
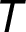 .
.
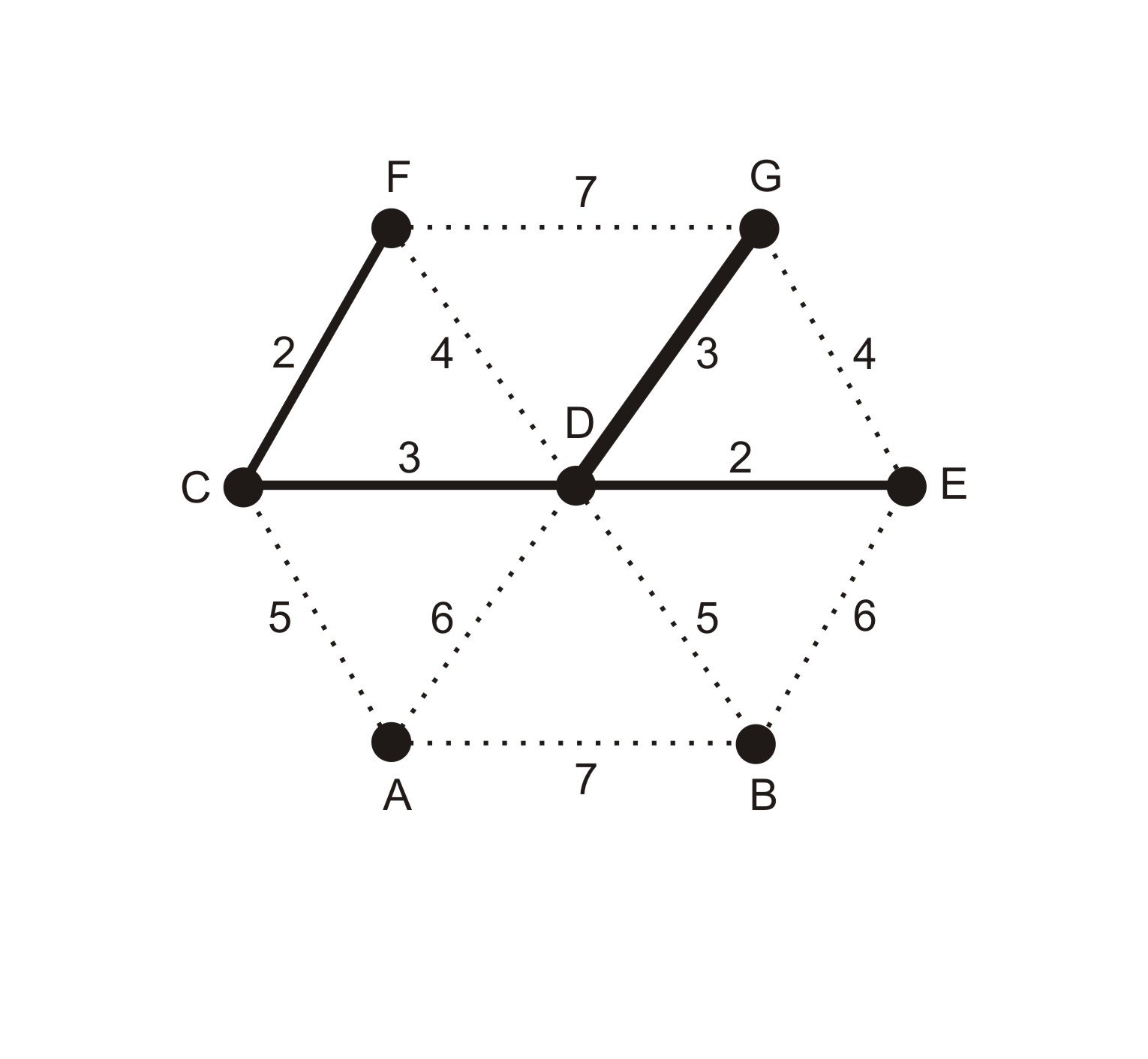
Při běžném provedení algoritmu pracujeme s vizuální reprezentací grafu.
Hrany, které přidáváme do kostry, zvýrazňujeme (barevně či jiným způsobem)
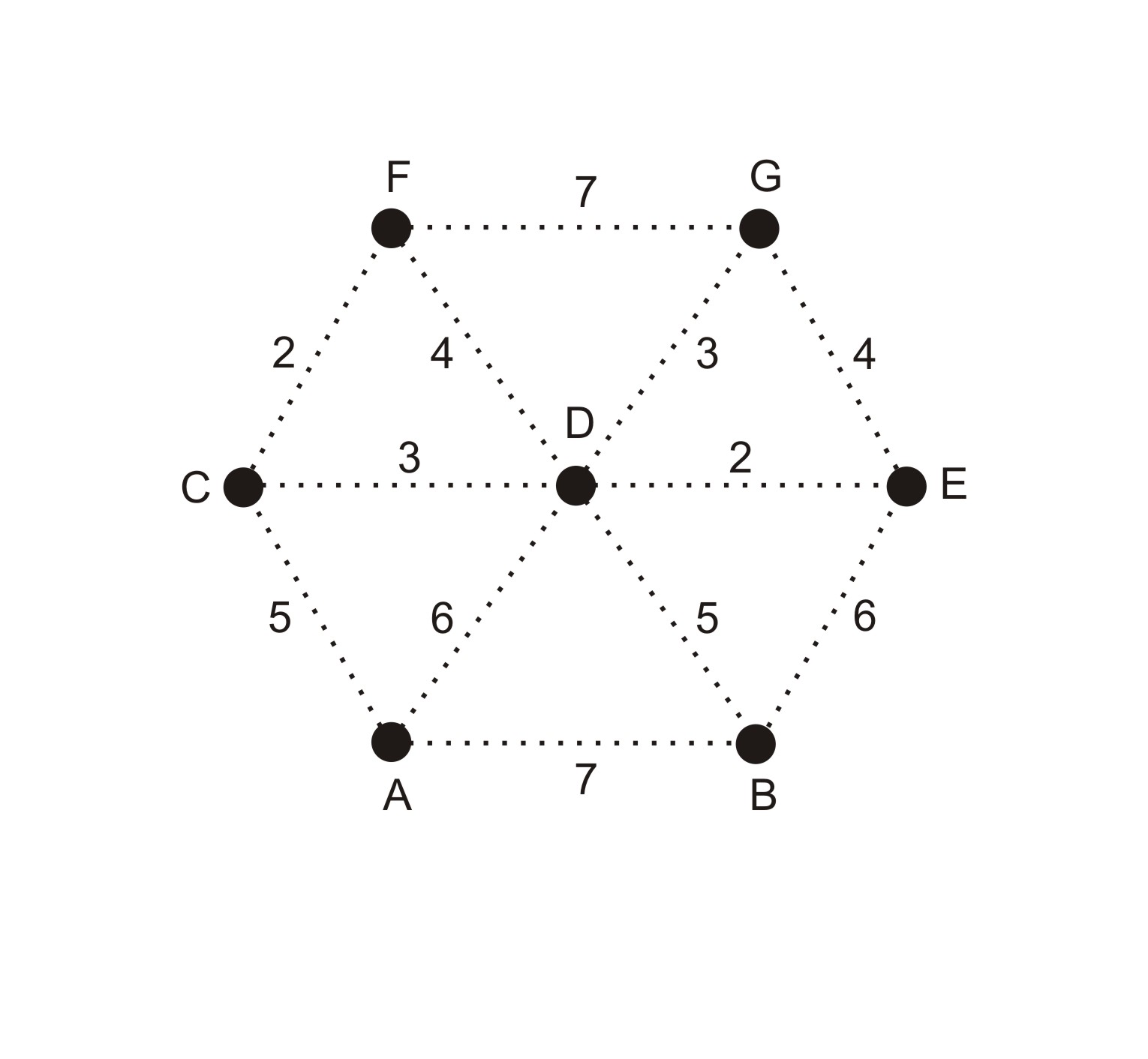
přímo v zadaném grafu. Na Obrázku 1 je znázorněn
graf 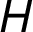 o sedmi vrcholech. Je ukázána situace před zpracováním 4. hrany v pořadí,
mezi uzly
o sedmi vrcholech. Je ukázána situace před zpracováním 4. hrany v pořadí,
mezi uzly  ,
,  . Po prvních třech krocích se do kostry
grafu vložily hrany
. Po prvních třech krocích se do kostry
grafu vložily hrany  ,
,  ,
,
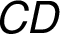 . Jelikož přidáním
hrany
. Jelikož přidáním
hrany  nevytvoříme kružnici, můžeme
ji taktéž vložit do kostry.
nevytvoříme kružnici, můžeme
ji taktéž vložit do kostry.
Příklad 1: Vážený neorientovaný graf 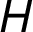
V dalším pokračování však do kostry grafu nemůžeme
přidat ani jednu hranu s ohodnocením 4, protože jejich
vložením by v obou případech vznikla kružnice
délky 3 (mezi trojicí 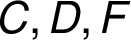 či
či 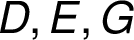 ).
).
Pro názornost uvádíme i konkrétní příklad váženého neorientovaného grafu a Animaci 1 naznačující výpočet minimální kostry pomocí Kruskalova algoritmu.
Příklad 2: Vážený neorientovaný graf 
-
- Počátek algoritmu - neorientovaný graf
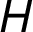 o sedmi uzlech
o sedmi uzlech 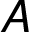 ,
, 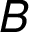 ,
,  ,
,  ,
,  ,
, 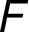 ,
, 
Hrany kostry: -
1/12
- Dosud nezpracované hrany:
 –
–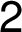 –
–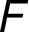 ,
,  –
–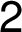 –
– ,
,  –
–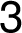 –
– ,
,  –
–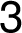 –
– ,
,  –
–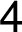 –
–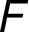 ,
,  –
–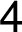 –
– ,
, 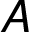 –
–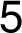 –
– ,
, 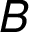 –
–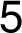 –
– ,
, 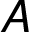 –
–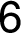 –
– ,
, 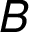 –
–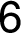 –
– ,
, 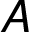 –
– –
–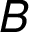 ,
, 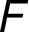 –
– –
–
Nezobrazovat tento popisek
2. Návrh možných adaptací
1. Organizace hran grafu v tabulce podle vrcholů, zápis kostry do dalšího dokumentu (listu):
Graf je nabízen ve formě tabulky.
Do jejího prvního sloupce zapisujeme návěští vrcholů.
Do dalších buněk na stejném řádku pro daný vrchol  vkládáme všechny
hrany vycházející z
vkládáme všechny
hrany vycházející z  , a to ve
formátu
, a to ve
formátu  –
–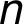 –
–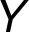 ,
kde
,
kde 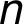 je
ohodnocení hrany a
je
ohodnocení hrany a
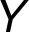 je koncový vrchol hrany.
je koncový vrchol hrany. 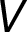 dalším listu tabulky,
případně v samostatném souboru, uchováváme hrany, které
zařazujeme do minimální kostry. Taktéž tam evidujeme množiny uzlů,
které jsou přidanými hranami propojeny. Uvažujme tentýž graf
dalším listu tabulky,
případně v samostatném souboru, uchováváme hrany, které
zařazujeme do minimální kostry. Taktéž tam evidujeme množiny uzlů,
které jsou přidanými hranami propojeny. Uvažujme tentýž graf 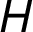 o sedmi uzlech,
který jsme znázornili na Obrázku 1. Následující dvě tabulky
(Tabulka 1 a Tabulka 2)
zachycují stav
po přidání prvních dvou hran do minimální kostry grafu
o sedmi uzlech,
který jsme znázornili na Obrázku 1. Následující dvě tabulky
(Tabulka 1 a Tabulka 2)
zachycují stav
po přidání prvních dvou hran do minimální kostry grafu 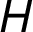 .
.
Příklad 3:
Graf 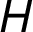 z Obrázku 1
po přidání dvou hran
z Obrázku 1
po přidání dvou hran
Příklad 4:
Kostra grafu 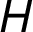 z Obrázku 1
po přidání dvou hran
z Obrázku 1
po přidání dvou hran
Z předchozích dvou tabulek je patrné, že obě dosud
přidané hrany propojují množiny uzlů 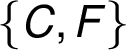 a
a 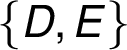 .
Před přidáním další hrany
v pořadí
.
Před přidáním další hrany
v pořadí 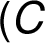 –
–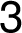 –
–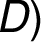 musíme ověřit,
zda v kostře grafu
musíme ověřit,
zda v kostře grafu 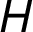 nevznikne kružnice. Vidomý student provádí
kontrolu vizuálně, nevidomý si k tomuto účelu eviduje množiny
uzlů propojených hranami dosavadní kostry. Pokud oba vrcholy
zpracovávané hrany patří do stejné množiny uzlů, jejím přidáním bychom
vytvořili kružnici.
nevznikne kružnice. Vidomý student provádí
kontrolu vizuálně, nevidomý si k tomuto účelu eviduje množiny
uzlů propojených hranami dosavadní kostry. Pokud oba vrcholy
zpracovávané hrany patří do stejné množiny uzlů, jejím přidáním bychom
vytvořili kružnici.  opačném případě aktualizujeme Tabulku 3. Aktuální
hranu vkládáme do kostry a následně upravíme množiny vzájemně propojených uzlů.
Nesmíme zapomenout, že právě zpracovaná hrana
byla v Tabulce 2 uvedena dvakrát, je tudíž nutné
oba výskyty vymazat.
opačném případě aktualizujeme Tabulku 3. Aktuální
hranu vkládáme do kostry a následně upravíme množiny vzájemně propojených uzlů.
Nesmíme zapomenout, že právě zpracovaná hrana
byla v Tabulce 2 uvedena dvakrát, je tudíž nutné
oba výskyty vymazat.
2. Organizace hran ve dvou sloupcích tabulky, zápis kostry do dalšího dokumentu (listu):
Graf je opět nabízen ve formě tabulky,
hrany jsou však organizovány jiným způsobem.
V 1. sloupci je jejich charakteristika,
opět ve formátu
 –
–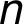 –
–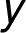 ,
kde
,
kde 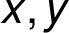 označují uzly propojené
hranou s ohodnocením
označují uzly propojené
hranou s ohodnocením 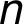 . Ve 2. sloupci je znovu
zopakováno ohodnocení hrany. Ukázku tohoto způsobu organizace
hran nabízíme v Tabulce 3 .
. Ve 2. sloupci je znovu
zopakováno ohodnocení hrany. Ukázku tohoto způsobu organizace
hran nabízíme v Tabulce 3 .
Příklad 5:
Hrany grafu 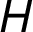 z Obrázku 1
včetně ohodnocení
z Obrázku 1
včetně ohodnocení
Většina tabulkových procesorů nabízí možnost seřadit data podle hodnot určitého sloupce. Nevidomý student tedy může hrany seřadit vzestupně podle ohodnocení, když je uspořádá podle 2. sloupce. Pro zápis kostry grafu a množin dosud propojených uzlů používáme buď druhý list tabulky či samostatný dokument. Postupujeme stejným způsobem jako v předchozí metodě.
3. Diskuze nad výhodami a nevýhodami
Poznamenejme rovnou, že druhou adaptaci nevidomí studenti hodnotili shodně jako lepší. Měli pro to tři hlavní důvody:
- ihned našli hranu, kterou mají aktuálně zpracovat;
- strávili méně času přesunem kurzoru mezi řádky a sloupci tabulky;
- nemuseli každou zpracovanou hranu dvakrát mazat ze zadání grafu.
U první metody studenti obtížně hledali hranu s aktuálně nejmenším ohodnocením.
Řešení může být následující. Hrany s nejmenším ohodnocením je možné vyhledat
postupným zadáváním řetězců "–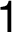 –", "–
–", "–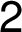 –", atd.
Jeden ze studentů
přišel s dalším nápadem, a to rezignovat na reprezentaci grafu formou
tabulky a využít podobným způsobem běžný textový editor, v němž hrany pro
daný uzel
–", atd.
Jeden ze studentů
přišel s dalším nápadem, a to rezignovat na reprezentaci grafu formou
tabulky a využít podobným způsobem běžný textový editor, v němž hrany pro
daný uzel  umístíme na samostatný řádek. Nevidomí studenti
tak plně mohou využít užitečných klávesových zkratek pro práci s textem i možností
brailleského řádku.
umístíme na samostatný řádek. Nevidomí studenti
tak plně mohou využít užitečných klávesových zkratek pro práci s textem i možností
brailleského řádku.