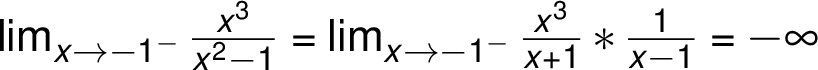Vyšetřování průběhu funkce
3. Ukázka provedení algoritmu nevidomým studentem
Ukázka je k dispozici v následujících formátech:
- přímo jako webová stránka
- soubor v BlindMoose:
analysis_cs_bm.doc - soubor v Lambdě:
analysis_cs.lambda - soubor MS Word:
analysis_cs.doc
Příklad
Vyšetřete průběh funkce
 .
.
Řešení
1. Definiční obor funkce

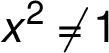
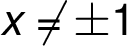

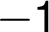 and
and 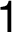 jsou body nespojitosti.
jsou body nespojitosti.
2. Sudá, lichá funkce

Funkce je lichá.
3. Určení, kdy je graf funkce nad (resp. pod) osou 
Řešíme rovnici 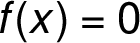 :
:





4. Monotónnost a body podezřelé z (lokálního) extrému
Řešíme rovnici 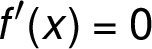 :
:


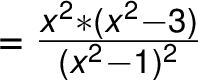
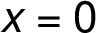

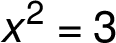





Lokální maximum: ![[-\sqrt{ 3}, \frac{ -3\sqrt{ 3}}{ 2}] [-\sqrt{ 3}, \frac{ -3\sqrt{ 3}}{ 2}]](/amalg/www/images/latex/___lL__d__s_sqrt_L_3_R_,_s_frac_L__d_3_s_sqrt_L_3__norm14_.png)
Lokální minimum: ![[\sqrt{ 3}, \frac{ 3\sqrt{ 3}}{ 2}] [\sqrt{ 3}, \frac{ 3\sqrt{ 3}}{ 2}]](/amalg/www/images/latex/___lL__s_sqrt_L_3_R_,_s_frac_L_3_s_sqrt_L_3_R__R___norm14_.png)
5. Úseky konkávnosti a konvexnosti
Řešíme rovnici  :
:

![=\frac{ 2x *(x^2 -1) *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^4} =\frac{ 2x *(x^2 -1) *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^4}](/amalg/www/images/latex/___e__s_frac_L_2x_S__l_x_P_2_d_1_r__S__lL__l_2x_P__norm14_.png)
![=\frac{ 2x *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^3} =\frac{ 2x *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL__l_2x_P_2_d_3_r__S__l_x_P__norm14_.png)
![=\frac{ 2x *[2x^4 -3x^2 -2x^2 +3 -2x^4 +6x^2]}{ (x^2 -1)^3} =\frac{ 2x *[2x^4 -3x^2 -2x^2 +3 -2x^4 +6x^2]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL_2x_P_4_d_3x_P_2_d_2x_P_2_p_norm14_.png)
![=\frac{ 2x *[x^2 +3]}{ (x^2 -1)^3} =\frac{ 2x *[x^2 +3]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL_x_P_2_p_3_rR__R__L__l_x_P__norm14_.png)


 :
:  , A
, A
 :
:  , V
, V
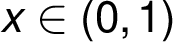 :
:  , A
, A
 :
:  , V
, V
The inflexním bodem je bod ![[0, 0] [0, 0]](/amalg/www/images/latex/___lL_0,0_rR____norm14_.png) .
.
6. Asymptoty
Asympota se směrnicí 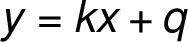 :
:








Asymptotou se směrnicí je přímka 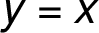 .
.
Asymptoty bez směrnice:
Asymptotami bez směrnice jsou přímky: 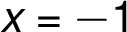 a
a 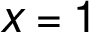 .
.
7. Závěrečný popis grafu
Funkce je definována pro  .
Graf je omezen asymptotami bez směrnice
.
Graf je omezen asymptotami bez směrnice 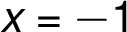 a
a 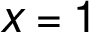 a asymptotou se směrnicí
a asymptotou se směrnicí
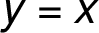 . Graf má dále dva lokální extrémy,
lokální maximum:
. Graf má dále dva lokální extrémy,
lokální maximum: ![[-\sqrt{ 3 }, \frac{ -3 \sqrt{ 3 } }{ 2 }] [-\sqrt{ 3 }, \frac{ -3 \sqrt{ 3 } }{ 2 }]](/amalg/www/images/latex/___lL__d__s_sqrt_L_3_R_,_s_frac_L__d_3_s_sqrt_L_3__norm14_.png) a lokální minimum:
a lokální minimum: ![[\sqrt{ 3 }, \frac{ 3 \sqrt{ 3 } }{ 2 }] [\sqrt{ 3 }, \frac{ 3 \sqrt{ 3 } }{ 2 }]](/amalg/www/images/latex/___lL__s_sqrt_L_3_R_,_s_frac_L_3_s_sqrt_L_3_R__R___norm14_.png) .
.
Graf funkce leží pro interval  pod osou
pod osou  , má lokální maximum v bodě
, má lokální maximum v bodě
![[-\sqrt{ 3 }, \frac{ -3 \sqrt{ 3 } }{ 2 }] [-\sqrt{ 3 }, \frac{ -3 \sqrt{ 3 } }{ 2 }]](/amalg/www/images/latex/___lL__d__s_sqrt_L_3_R_,_s_frac_L__d_3_s_sqrt_L_3__norm14_.png) ,
má konkávní tvar a leží vlevo od asymptoty
,
má konkávní tvar a leží vlevo od asymptoty 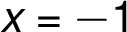 . Ypsylonová souřadnice asymptoty
. Ypsylonová souřadnice asymptoty
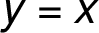 v bodě
v bodě  je
je
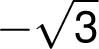 , což je více
než
, což je více
než  , tedy funkční hodnota maxima.
Graf funkce
, tedy funkční hodnota maxima.
Graf funkce 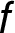 se v intervalu
se v intervalu
 nachází pod asymptotou
nachází pod asymptotou 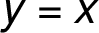 .
.
Graf funkce v intervalu 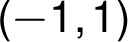 prochází průsečíkem s osami
prochází průsečíkem s osami  a
a
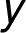 v bodě
v bodě ![[0, 0] [0, 0]](/amalg/www/images/latex/___lL_0,0_rR____norm14_.png) ,
tento bod je současně také inflexní.
Graf funkce zde mění svůj tvar z konvexního na konkávní,
funkce se nachází mezi asymptotami
,
tento bod je současně také inflexní.
Graf funkce zde mění svůj tvar z konvexního na konkávní,
funkce se nachází mezi asymptotami 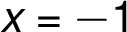 a
a
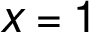 , asymptota
, asymptota 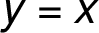 kříží graf funkce
v bodě
kříží graf funkce
v bodě ![[0, 0] [0, 0]](/amalg/www/images/latex/___lL_0,0_rR____norm14_.png) .
.
Graf funkce v intervalu 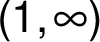 leží
celý nad osou
leží
celý nad osou  , má lokální minimum v bodě
, má lokální minimum v bodě
![[\sqrt{ 3 }, \frac{ 3 \sqrt{ 3 } }{ 2 }] [\sqrt{ 3 }, \frac{ 3 \sqrt{ 3 } }{ 2 }]](/amalg/www/images/latex/___lL__s_sqrt_L_3_R_,_s_frac_L_3_s_sqrt_L_3_R__R___norm14_.png) , má konvexní tvar
a leží vpravo od asymptoty
, má konvexní tvar
a leží vpravo od asymptoty 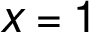 .
Ypsylonová souřadnice asymptoty
.
Ypsylonová souřadnice asymptoty 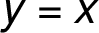 v bodě
v bodě
 je
je 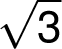 ,
což je méně než
,
což je méně než  ,
tedy funkční hodnota minima.
Graf funkce
,
tedy funkční hodnota minima.
Graf funkce 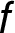 se v intervalu
se v intervalu 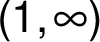 nachází nad asymptotou
nachází nad asymptotou 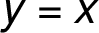 .
.

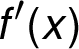 kladná či
záporná
kladná či
záporná 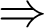 kdy je
kdy je 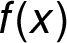 rostoucí či klesající;
určení lokálních extrémů;
rostoucí či klesající;
určení lokálních extrémů;
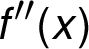 kladná či
záporná
kladná či
záporná  a řešení nevidomého studenta, který vyšetřoval její průběh.
Klíčovou otázkou je adaptace 7. úkolu, tj. vykreslení grafu funkce na základě vypočítaných informací.
Více se tomuto problému věnujeme v části
a řešení nevidomého studenta, který vyšetřoval její průběh.
Klíčovou otázkou je adaptace 7. úkolu, tj. vykreslení grafu funkce na základě vypočítaných informací.
Více se tomuto problému věnujeme v části