Dijkstrův algoritmus
2. Návrh možných adaptací
1. Práce s grafem v jednom listu tabulkového procesoru:
Do prvního sloupce zapisujeme návěští jednotlivých uzlů počínaje iniciálním uzlem. Do dalších buněk na stejném řádku pro uzel X zapisujeme všechny hrany z něj vycházející, a to ve formátu n–Y, kde n je ohodnocení hrany, Y je koncový uzel hrany, viz Tabulka 1.
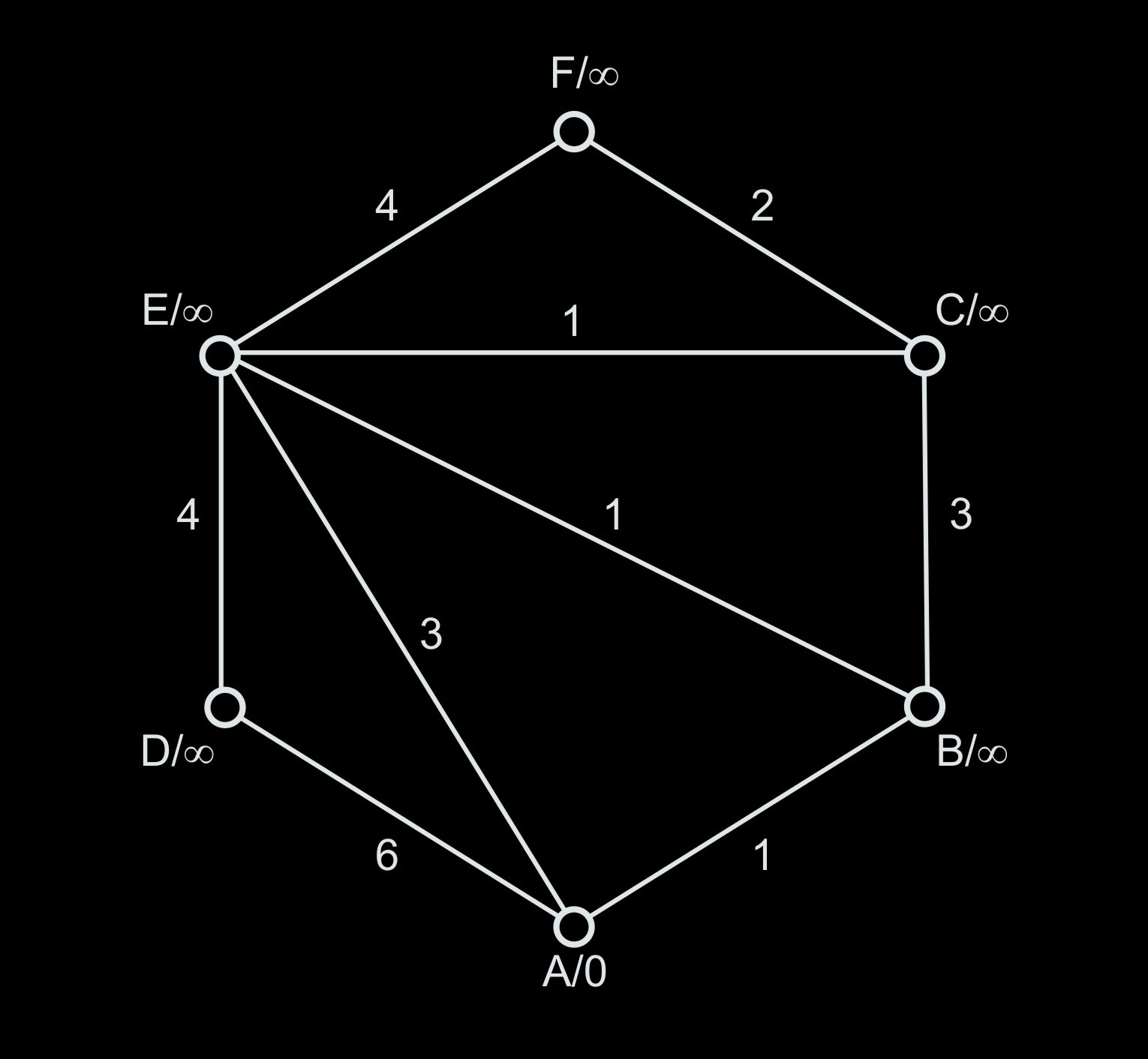
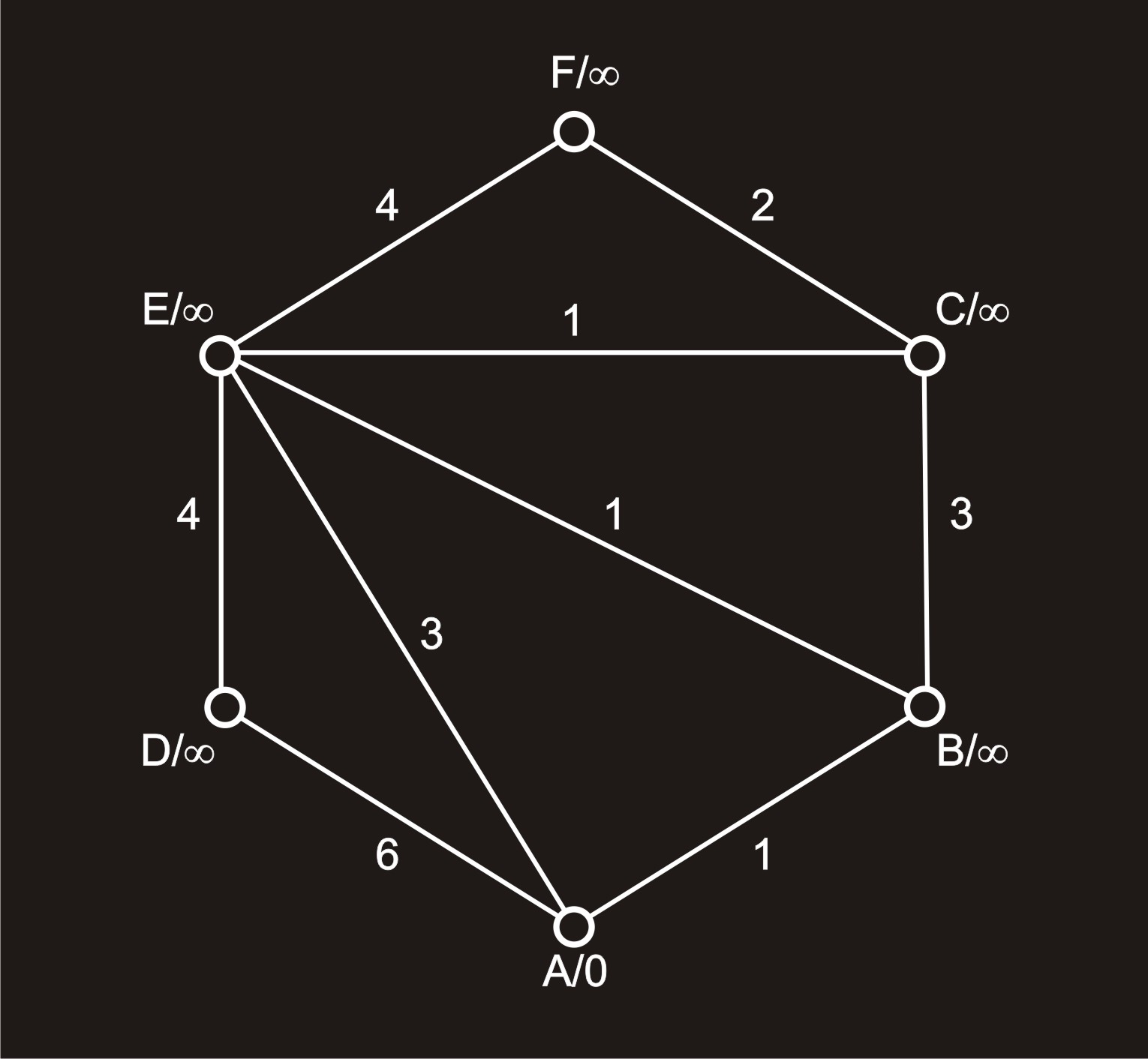
Příklad 1: Neorientovaný graf G z Obrázku 1
| A/0 | 1–B | 3–E | 6–D | ||
| B/\infty | 1–A | 1–E | 3–C | ||
| C/\infty | 1–E | 2–F | 3–B | ||
| D/\infty | 4–E | 6–A | |||
| E/\infty | 1–B | 1–C | 3–A | 4–D | 4–F |
| F/\infty | 2–C | 4–E |
Editujeme pouze návěští uzlů v 1. sloupci, hodnoty v ostatních sloupcích slouží pouze pro čtení. Zpracovaný uzel označujeme hvězdičkou, abychom jej při dalším pokračování algoritmu nemuseli brát v potaz. Algoritmus končí, jakmile máme všechny uzly označené hvězdičkou (jsou tedy všechny zpracované).
2. Práce s grafem ve dvou listech tabulkového procesoru:
Oproti předchozí metodě dochází k jediné změně. 1. list používáme pouze pro čtení hran, na 2. listu máme pouze sloupec s návěštími uzlů, které postupně upravujeme.
3. Práce s grafem ve formě hmatového obrázku, zápis vzdáleností uzlů v libovolném editoru:
Metoda je podobná předchozímu postupu s tím rozdílem, že graf je nabízen v podobě hmatového obrázku. Student tak kombinuje čtení hmatem s editací návěští jednotlivých uzlů zapsaných v libovolném textovém či tabulkovém editoru.