Ford-Fulkersonův algoritmus
1. Popis standardní metody algoritmu
Ford-Fulkersonův algoritmus slouží k vyhledání maximálního toku
v síti (Síť je orientovaný graf,
kde ohodnocení každé hrany znamená maximální množství energie,
které skrze hranu může procházet).
Pracujeme tedy se sítí 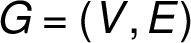 ,
kde
,
kde 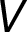 je množina vrcholů včetně zdroje
je množina vrcholů včetně zdroje 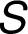 a stoku
a stoku 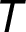 ,
,  je množina orientovaných hran.
Návěští každé hrany zapisujeme ve formátu
je množina orientovaných hran.
Návěští každé hrany zapisujeme ve formátu 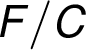 ,
kde
,
kde  značí její kapacitu a
značí její kapacitu a 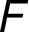 tok,
tj. množství energie, které v ní proudí.
tok,
tj. množství energie, které v ní proudí.
- Na počátku algoritmu nastavíme u všech hran nulový tok.
- Opakovaně hledáme nenasycenou cestu od zdroje ke stoku. Jakmile ji nalezneme, zjistíme minimální rezervu kapacity všech jejích hran, o kterou následně navýšíme tok v síti.
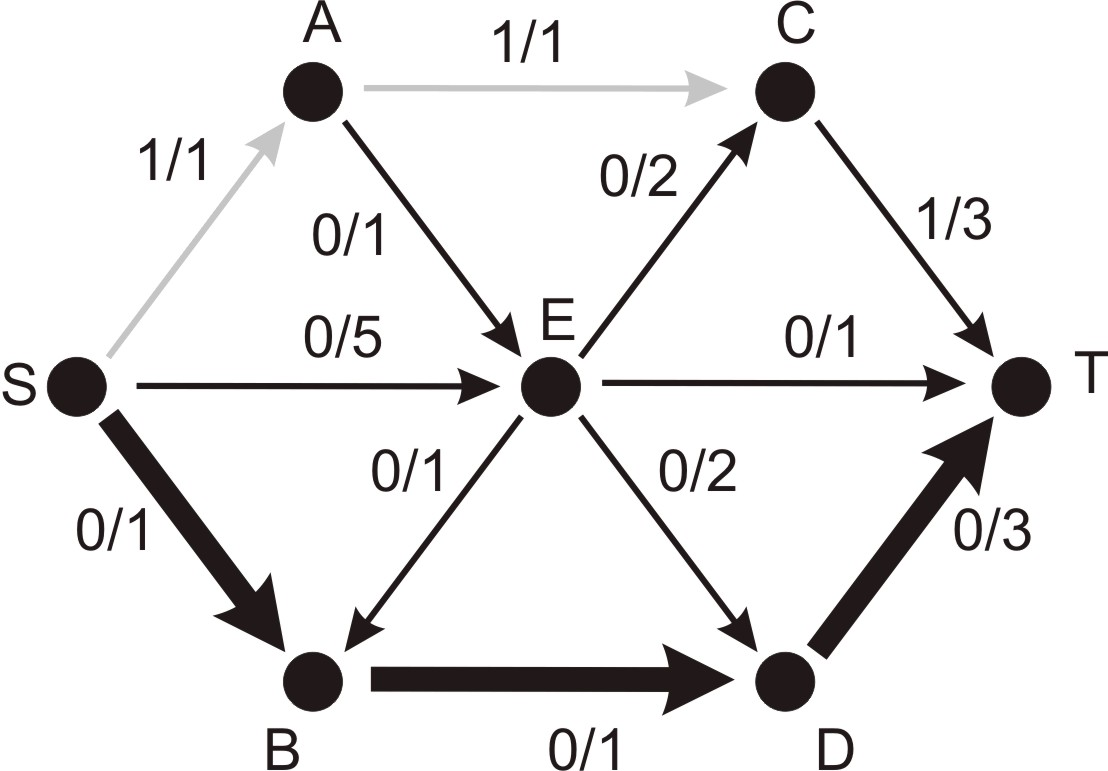
Při běžném provedení algoritmu pracujeme s vizuální reprezentací sítě,
u níž měníme návěští hran. Na Obrázku 1 je
znázorněna síť 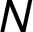 o sedmi
vrcholech s aktuálním tokem 1 (viz cesta
o sedmi
vrcholech s aktuálním tokem 1 (viz cesta 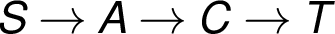 ). Je zvýrazněna
nenasycená cesta
). Je zvýrazněna
nenasycená cesta 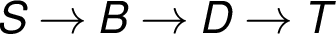 , u níž je minimální rezerva kapacity
hran rovna 1. Můžeme tedy v dalším kroku zvýšit tok v síti a upravit
návěští hran nenasycené cesty, tj. modifikovat
, u níž je minimální rezerva kapacity
hran rovna 1. Můžeme tedy v dalším kroku zvýšit tok v síti a upravit
návěští hran nenasycené cesty, tj. modifikovat 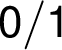 na
na
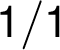 v případě
hran
v případě
hran 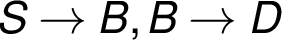 a
a
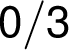 na
na 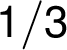 u hrany
u hrany
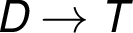 .
.
Pro názornost uvádíme i konkrétní příklad sítě a Animaci 1 naznačující výpočet maximálního toku pomocí Ford-Fulkersonova algoritmu.
Příklad 2: síť 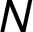
-
- Počátek algoritmu – síť
 o sedmi uzlech
o sedmi uzlech  ,
, 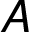 ,
, 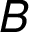 ,
,  ,
,  ,
,  ,
, 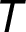
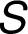 :
: 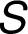 –
–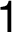 –
–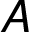
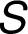 –
–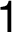 –
–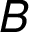
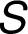 –
–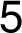 –
–
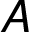 :
: 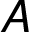 –
–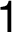 –
–
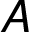 –
–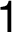 –
–
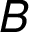 :
: 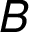 –
–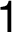 –
–
 :
:  –
–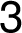 –
–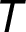
 :
:  –
–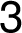 –
–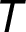
 :
:  –
–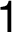 –
–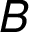
 –
–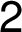 –
–
 –
–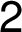 –
–
 –
–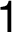 –
–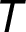
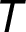 Nezobrazovat tento popisek
Nezobrazovat tento popisek
2. Návrh možných adaptací
1. Práce se sítí v jednom listu tabulkového procesoru:
Síť je opět nabízena ve formě tabulky a organizována podobným způsobem
jako v případě 1. metody
adaptace Dijkstrova algoritmu.
V prvním sloupci jsou vypsány uzly sítě,
do dalších buněk na stejném řádku pro daný uzel  zapisujeme všechny hrany, které začínají v uzlu
zapisujeme všechny hrany, které začínají v uzlu  .
Uvádíme je ve formátu
.
Uvádíme je ve formátu 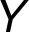 –
–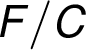 ,
kde
,
kde 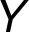 je uzel, ve kterém orientovaná hrana z
je uzel, ve kterém orientovaná hrana z  končí,
končí,
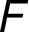 je aktuální tok skrze hranu a
je aktuální tok skrze hranu a  je
její kapacita. Uvažujme tutéž síť
je
její kapacita. Uvažujme tutéž síť 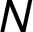 , jakou jsme znázornili
na Obrázku 1.
Následující Tabulka 1 zachycuje fázi algoritmu,
při níž jsme již nalezli jednu nenasycenou cestu
, jakou jsme znázornili
na Obrázku 1.
Následující Tabulka 1 zachycuje fázi algoritmu,
při níž jsme již nalezli jednu nenasycenou cestu 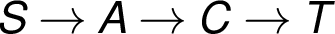 .
.
Příklad 3: síť 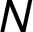
Nevidomý student nejprve najde nenasycenou cestu od
zdroje 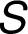 ke stoku
ke stoku 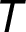 .
Prochází postupně tabulkou a pamatuje si posloupnost uzlů,
kterými cesta vede, i aktuální minimální rezervu jejích hran. Ve druhém průchodu již upravuje tok a nasycené hrany
označuje hvězdičkou.
.
Prochází postupně tabulkou a pamatuje si posloupnost uzlů,
kterými cesta vede, i aktuální minimální rezervu jejích hran. Ve druhém průchodu již upravuje tok a nasycené hrany
označuje hvězdičkou.
2. Organizace hran pod sebou na jednotlivých řádcích v běžném textovém editoru:
Každou hranu zapisujeme na samostatném řádku ve formátu  –
–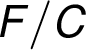 –
–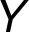 ,
kde
,
kde  je
počáteční uzel hrany,
je
počáteční uzel hrany, 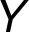 koncový uzel hrany,
koncový uzel hrany,
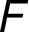 aktuální tok skrze hranu a
aktuální tok skrze hranu a
 její kapacita. Hrany řadíme abecedně dle uzlu, ze kterého vycházejí.
Pracujeme s nimi obdobným způsobem jako u první metody, tj. procházíme hrany
vždy dvakrát, poprvé, abychom nalezli nenasycenou cestu od zdroje ke stoku,
podruhé, abychom upravili tok na této cestě.
její kapacita. Hrany řadíme abecedně dle uzlu, ze kterého vycházejí.
Pracujeme s nimi obdobným způsobem jako u první metody, tj. procházíme hrany
vždy dvakrát, poprvé, abychom nalezli nenasycenou cestu od zdroje ke stoku,
podruhé, abychom upravili tok na této cestě.
3. Diskuze nad výhodami a nevýhodami
V tomto případě u nevidomých studentů zvítězila 1. metoda. Nebylo příliš složité se orientovat v tabulce a hledat nenasycenou cestu (Poznamenejme, že problém nastává ve chvíli, kdy je k nalezení maximálního toku nutné některé hrany procházet proti směru toku.). Nevýhodou druhé metody je fakt, že při hledání nenasycené cesty musí nevidomý často projít mnoha řádky s údaji, které jsou pro něj v tu chvíli nepodstatné. U obou nabízených adaptací se jeví jako vhodné poznamenat si zpracovávanou nenasycenou cestu např. do textového editoru (stačí vypsat posloupnost vrcholů od zdroje ke stoku).

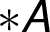 –
–
 –
–