Zásady pro tvorbu adaptace
Úvodní shrnutí
Při praktické výuce jsme často řešili úkol, jak daný matematický algoritmus adaptovat pro nevidomého studenta. Z našich zkušeností vyplývá, že je vhodné držet se několika zásad, které zde nejprve souhrnně uvádíme a následně vysvětlíme jejich význam:
- Respektování způsobu práce nevidomého
- Případná změna uspořádání objektů, které se v algoritmu objevují
- Snaha o efektivní způsob provedení algoritmu bez přílišných nároků na paměť i čas
- Volba vhodného formátu pro práci s daty a objekty algoritmu
- Srozumitelnost zapsaného výpočtu opravujícímu
Uspořádání objektů algoritmu
Způsob vnímání informací je u nevidomého zcela odlišný v porovnání s lidmi, kteří svůj zrak mohou plně využít. Při práci s matematickým algoritmem či textem se zpravidla používá prostorové uspořádání objektů takové, že jejich vzájemná poloha vyjadřuje vztahy mezi nimi. Pozice objektu nám usnadní jeho nalezení a následné prozkoumání jeho detailů, se kterými dále pracujeme. Takové prostorové uspořádání však může být a často bývá (paradoxně v době informačních technologií) pro nevidomého spíše překážkou. Při snaze nalézt určitou informaci často postupně prochází i jiné, v tu chvíli nepodstatné, objekty včetně jejich detailů, což jej neúměrně časově i paměťově zaměstnává. Chybí mu tak možnost vnímat objekty jako celky a abstrahovat se od jejich konkrétních hodnot či vlastností.
Příklad
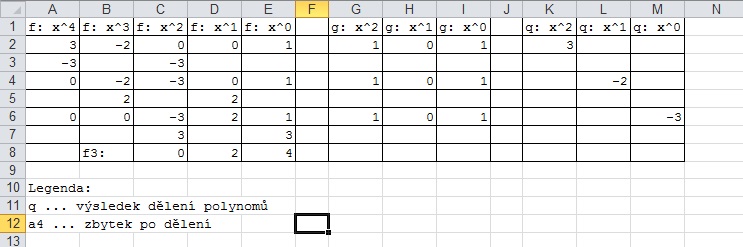
Názorně to vysvětlíme na dobře známém algoritmu pro dělení polynomu polynomem, jehož popis nabízíme v části Algoritmy a jejich adaptace. Jedna z jeho navržených adaptací (Zápis polynomů pouze pomocí koeficientů v tabulkovém procesoru) důsledně respektuje uspořádání všech tří polynomů, se kterými se pracuje, pouze dílčí výsledky jsou uváděny pouze jako koeficienty členů, viz následující obrázek.
Odkaz na excelovskou tabulku s daty:
polynomial_division_cs.xls
Potřebuje-li například nevidomý uživatel vydělit vedoucí koeficienty obou polynomů (na obr. dělenec $f$ a dělitel $g$), naráží na několik komplikací:
- dosažitelnost jednotlivých koeficientů není snadná – při pohybu kurzorem po buňkách tabulky nemá možnost ignorovat konkrétní hodnoty, které ho v tu chvíli nezajímají.
- V tabulce se navíc těžko orientuje a často musí ověřovat, s jakou mocninou je daný koeficient spojen.
- Chce-li ušetřit čas, tak je neustále zaměstnán udržováním mezivýsledků ve své paměti při současném hledání pozice, na kterou je může vložit.
Chceme-li při adaptaci matematického algoritmu respektovat způsob práce nevidomého s informacemi, je nutné, abychom mu vždy zajistili snadnou a rychlou dosažitelnost objektů, se kterými má aktuálně pracovat. Snaha dodržovat jejich rovinné (prostorové) uspořádání proto nebývá pro nevidomého vždy účelná, i když při prvotním seznámení s algoritmem mu může pomoci k lepšímu pochopení jednotlivých kroků výpočtu.
Volba vhodných nástrojů
Kromě zvolené metody adaptace bychom také měli zvážit, jaké (počítačové) nástroje jsou vhodné pro manipulaci s daty algoritmu a samotný výpočet. Někdy postačí otevřít jediný soubor v běžném textovém editoru. Další možností je práce s tabulkovým procesorem, ve kterém jsou data uspořádána do řádků a sloupců, navíc je možné pracovat s více listy v jednom souboru. Jak lze tušit, tento způsob se hodí pro manipulaci s maticemi. Existují samozřejmě další alternativy, za všechny jmenujme speciální matematický editor Lambda s podporou hlasového i hmatového výstupu, který nabízí nevidomým studentům užitečné kompenzační funkce, které jim usnadní práci se složitějšími matematickými výrazy či strukturami.
Srozumitelnost ostatním
V neposlední řadě je třeba zajistit, aby byl celý postup výpočtu pochopitelný i pro ty, kteří kontrolují a hodnotí práci nevidomého studenta. Adaptace nemusí respektovat původní uspořádání objektů, není tak často srozumitelná lidem, kteří jsou zvyklí na standardní způsob provedení algoritmu. Je tedy vhodné předem vysvětlit případné odchylky oproti původnímu konceptu.