Kruskalův algoritmus
1. Popis standardní metody algoritmu
Kruskalův algoritmus slouží k vyhledání minimální kostry grafu. Pracujeme s váženým neorientovaným grafem G = (V, E, w), kde V je množina vrcholů, E je množina neorientovaných hran a w je kladné ohodnocení hran.
- Na počátku algoritmu inicializujeme kostru T = (V, \emptyset) obsahující všechny vrcholy grafu G a prázdnou množinu hran.
- Seřadíme všechny hrany grafu G vzestupně dle jejich ohodnocení a v tomto pořadí je postupně zpracováváme.
- Pokud přidáním konkrétní hrany e do kostry T nevniká kružnice, přidáme e do T, v opačném případě hranu do T nepřidáme.
- Po zpracování poslední hrany s nejvyšším ohodnocením získáme minimální kostru T.
Při běžném provedení algoritmu pracujeme s vizuální reprezentací grafu. Hrany, které přidáváme do kostry, zvýrazňujeme (barevně či jiným způsobem) přímo v zadaném grafu. Na Obrázku 1 je znázorněn graf H o sedmi vrcholech. Je ukázána situace před zpracováním 4. hrany v pořadí, mezi uzly D, G. Po prvních třech krocích se do kostry grafu vložily hrany CF, DE, CD. Jelikož přidáním hrany DG nevytvoříme kružnici, můžeme ji taktéž vložit do kostry.
Příklad 1: Vážený neorientovaný graf H
V dalším pokračování však do kostry grafu nemůžeme přidat ani jednu hranu s ohodnocením 4, protože jejich vložením by v obou případech vznikla kružnice délky 3 (mezi trojicí C, D, F či D, E, G).
Pro názornost uvádíme i konkrétní příklad váženého neorientovaného grafu a Animaci 1 naznačující výpočet minimální kostry pomocí Kruskalova algoritmu.
Příklad 2: Vážený neorientovaný graf H
-
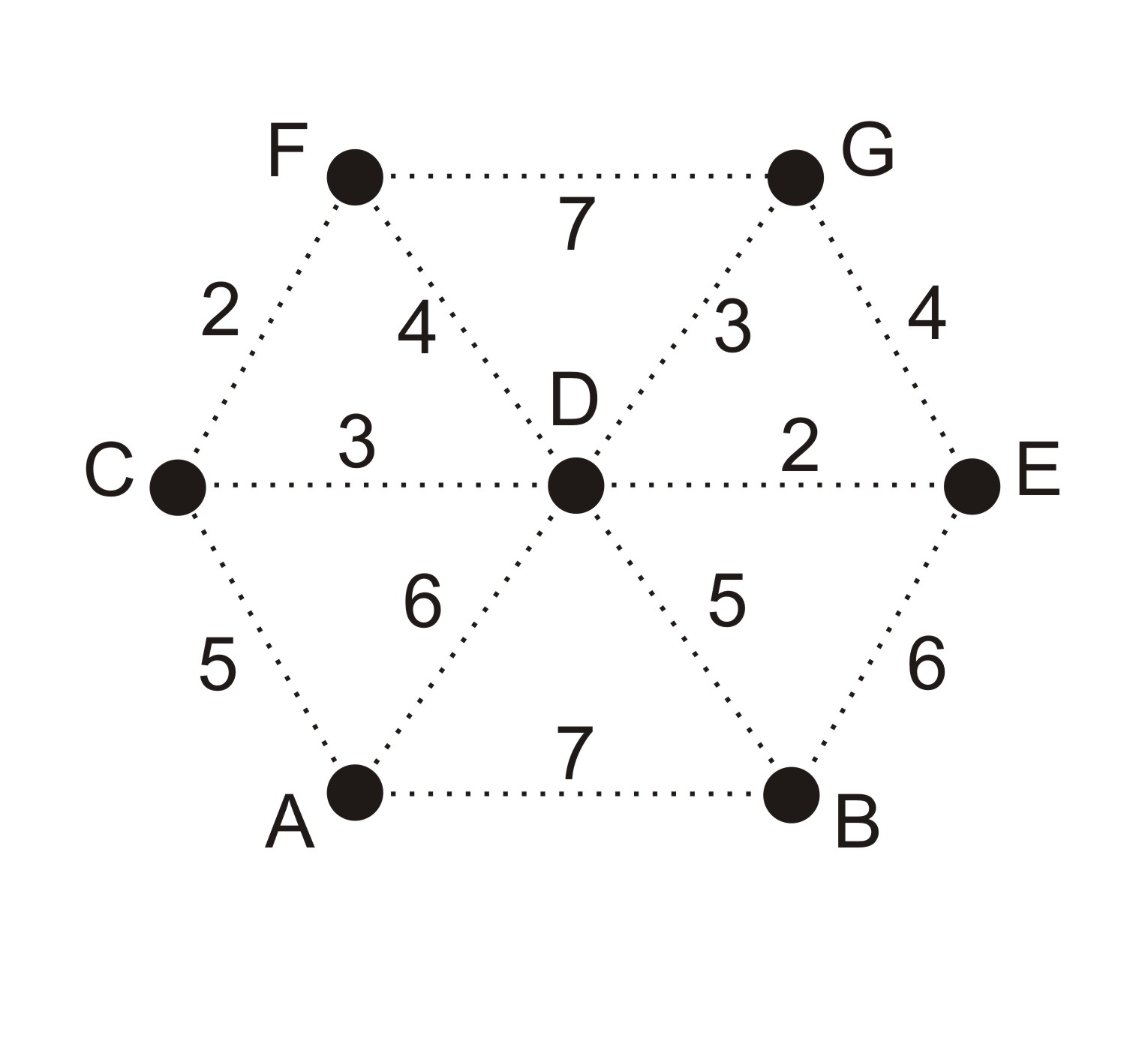
- Počátek algoritmu - neorientovaný graf H o sedmi uzlech A, B, C, D, E, F, G
Hrany kostry: - Dosud nezpracované hrany: C–2–F, D–2–E, C–3–D, D–3–G, D–4–F, E–4–G, A–5–C, B–5–D, A–6–D, B–6–E, A–7–B, F–7–G
Nezobrazovat tento popisek

