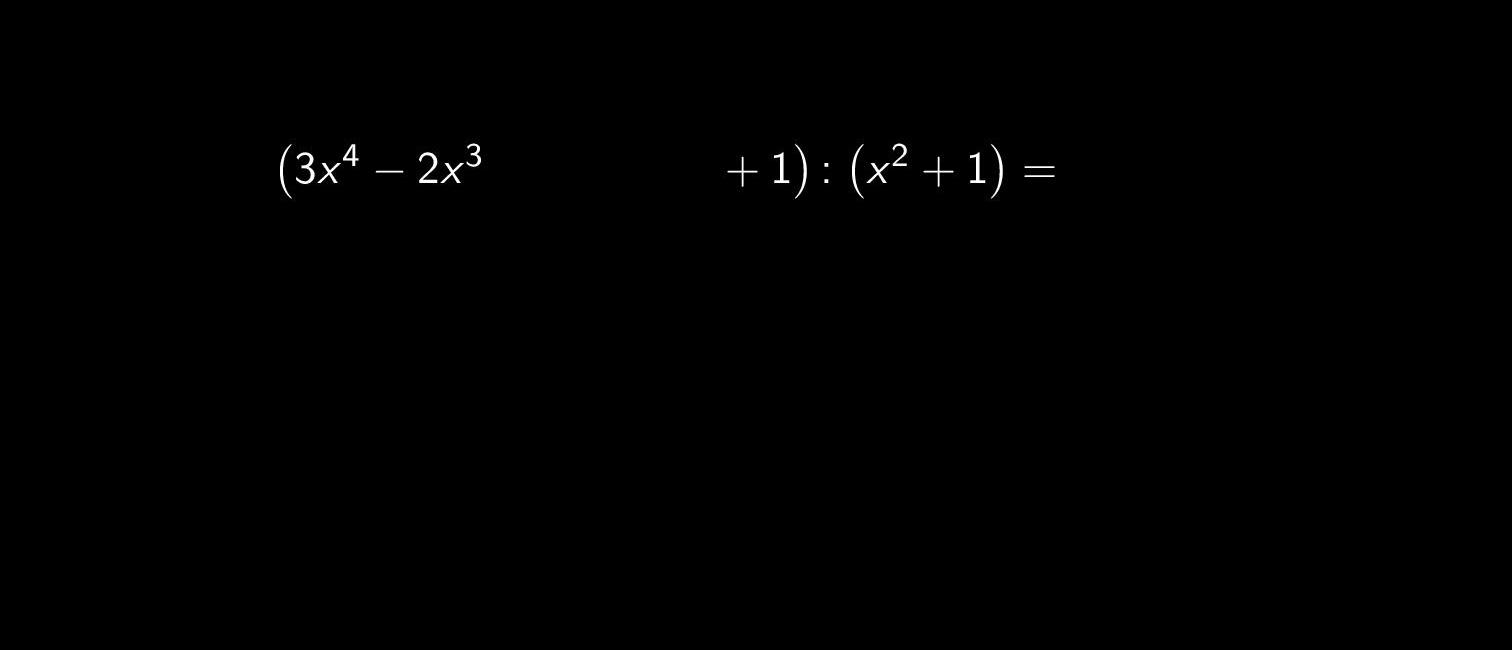Dělení polynomů
2. Návrh možných adaptací
1. Důsledné opisování veškerých podvýrazů:
Důsledné opisování veškerých podvýrazů, se kterými se v algoritmu pro dělení polynomů pracuje, včetně krátkého vysvětlení všech mezivýsledků, je ukázáno ve výpočtu v editoru Lambda na Obrázku 1:
Příklad 2: Dělení polynomů s pomocí lineárního zapisování
Odkaz na soubor ve formátu lambda:
polynomial_division_2_cs.lambda
2. Zápis polynomů pouze pomocí koeficientů v tabulkovém procesoru:
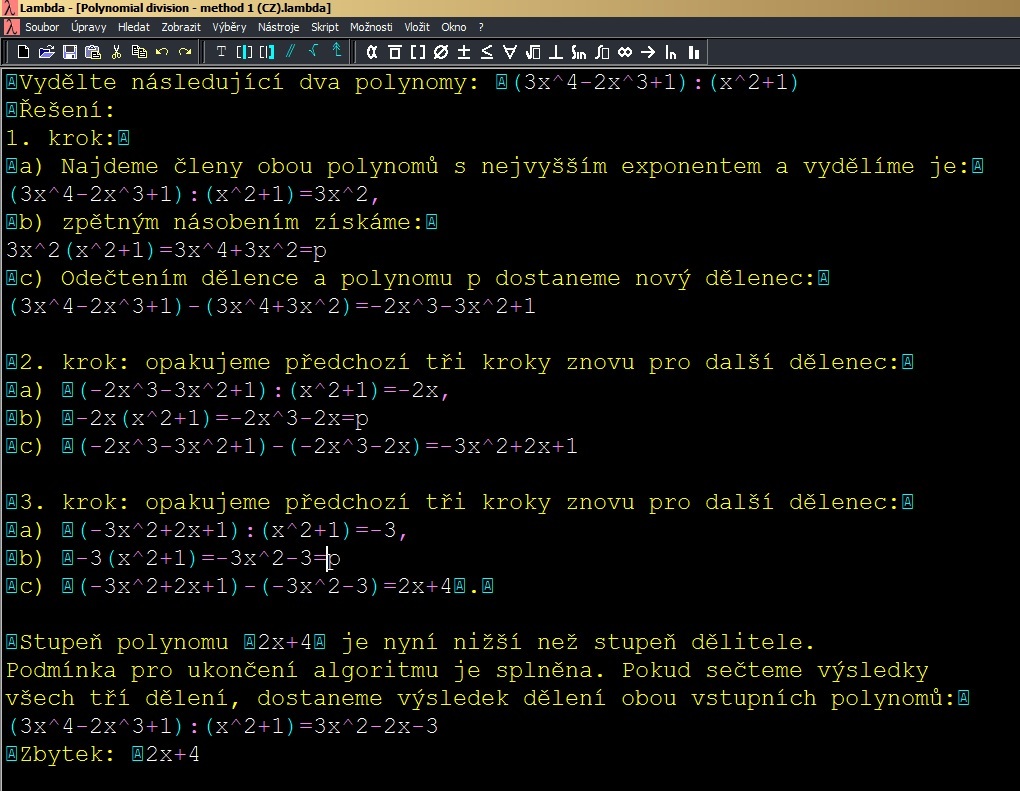
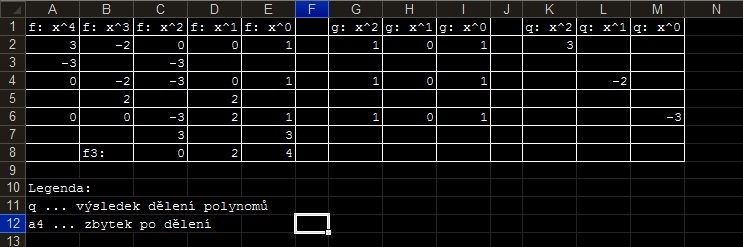
V prvním řádku tabulkového listu se zapisují pouze mocniny členů dělence, dělitele a podílu, přičemž se jednotlivé polynomy oddělí prázdnou buňkou. Na dalších řádcích se pod danou mocninu vkládá už pouze koeficient příslušného členu. V případě zápisu dalších polynomů f_1, f_2, \dots, f_n, f_{ n+1 } nižšího stupně, které vznikají zpětným násobením dělitele a aktuálního dílčího členu q_i výsledného podílu, se využívá dalších řádků pod dělencem. Viz ukázka výpočtu v editoru MS Excel na Obrázku 2:
Příklad 3: Dělení polynomů s pomocí tabulkového procesoru
Odkaz na soubor ve formátu MS Excel:polynomial_division_3_cs.xls
3. Zápis veškerých polynomů pod sebou v jednom (textovém) editoru:
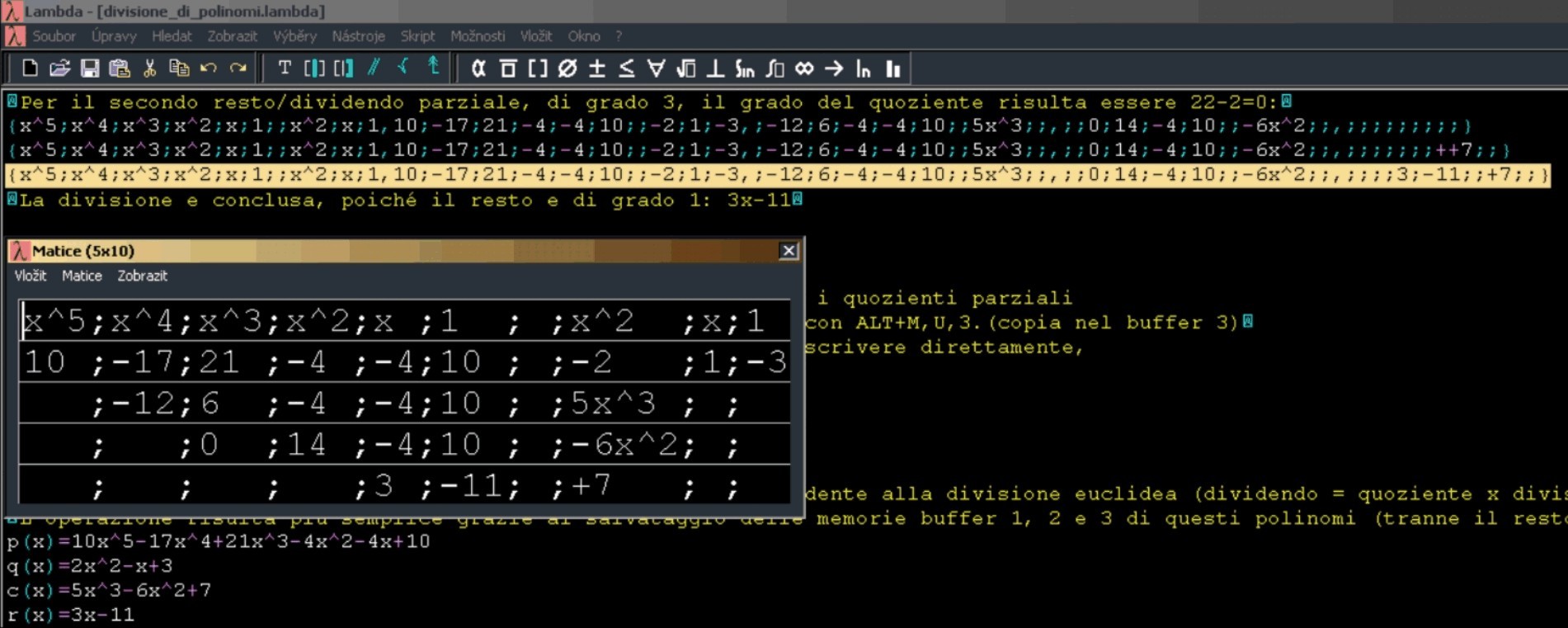
Následující metoda je založena na tom, že polynomy, se kterými nevidomý student aktuálně pracuje, si nechává vždy na sousedních řádcích, aby se mezi nimi mohl snadno pohybovat, a to pouze jedním stiskem klávesy šipka dolů či šipka nahoru. Viz ukázka výpočtu v editoru Lambda (Animace 2):
Příklad 4: Adaptace na konkrétním polynomu
-
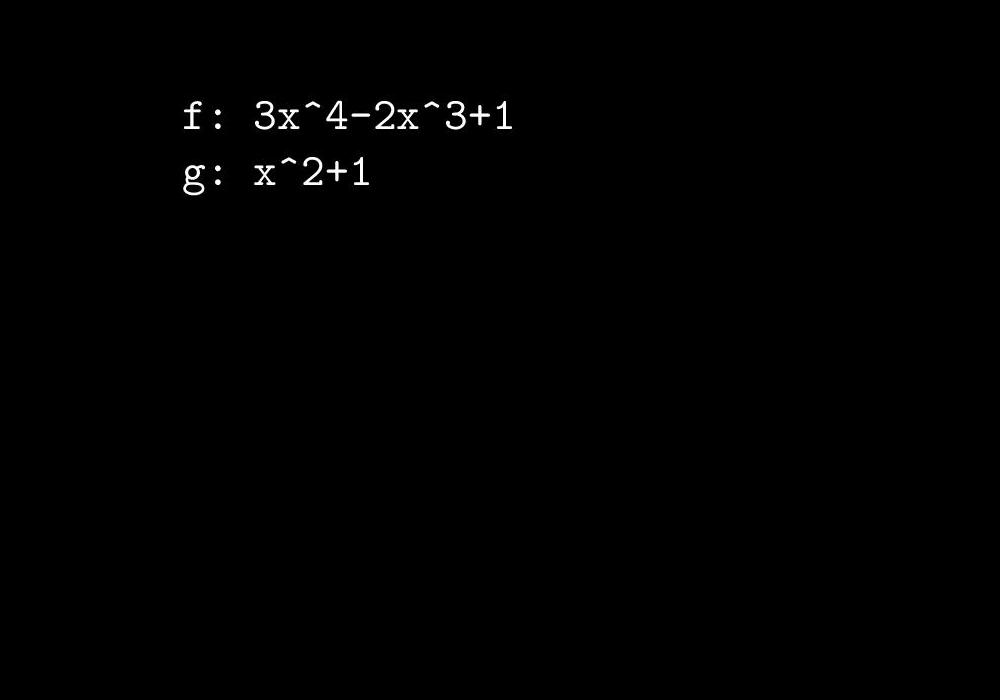
- Zapsání obou polynomů f, g (dělence i dělitele) pod sebe
- f: 3x^4 - 2x^3 + 1
g: x^2+1 Nezobrazovat tento popisek
4. Zápis všech polynomů do tří souborů, případně listů tabulkového procesoru:
- do prvního samostatného souboru (případně listu) vkládáme na jednotlivé řádky postupně dělenec a polynomy f_1, f_2, \dots, f_n, f_{ n + 1} nižšího stupně, které vznikají zpětným násobením dělitele a aktuálního dílčího členu q_i výsledného polynomu. Respektujeme tak umístění zmíněných polynomů známé v případě standardního průběhu algoritmu. V případě použití tabulkového procesoru můžeme využít metodu zápisu polynomu pomocí jeho koeficientů.
- do druhého samostatného souboru (případně listu) umístíme pouze dělitele.
- do třetího samostatného souboru (případně listu) vkládáme postupně členy q_1, q_2, \dots, q_n výsledného podílu q = q_1 + q_2 + q_3 + \dots + q_n .
V průběhu výpočtu se pak přepínáme mezi jednotlivými soubory
(resp. listy) pomocí klávesové zkratky Alt+Tab (resp. Ctrl+PgUp,
Ctrl+PgDown) a upravujeme je s výjimkou dělitele, který zůstává stejný.