Kruskalův algoritmus
1. Popis standardní metody algoritmu
Kruskalův algoritmus slouží k vyhledání minimální kostry grafu. Pracujeme s váženým neorientovaným grafem $G = (V, E, w)$, kde $V$ je množina vrcholů, $E$ je množina neorientovaných hran a $w$ je kladné ohodnocení hran.
- Na počátku algoritmu inicializujeme kostru $T = (V, \emptyset)$ obsahující všechny vrcholy grafu $G$ a prázdnou množinu hran.
- Seřadíme všechny hrany grafu $G$ vzestupně dle jejich ohodnocení a v tomto pořadí je postupně zpracováváme.
- Pokud přidáním konkrétní hrany $e$ do kostry $T$ nevniká kružnice, přidáme $e$ do $T$, v opačném případě hranu do $T$ nepřidáme.
- Po zpracování poslední hrany s nejvyšším ohodnocením získáme minimální kostru $T$.
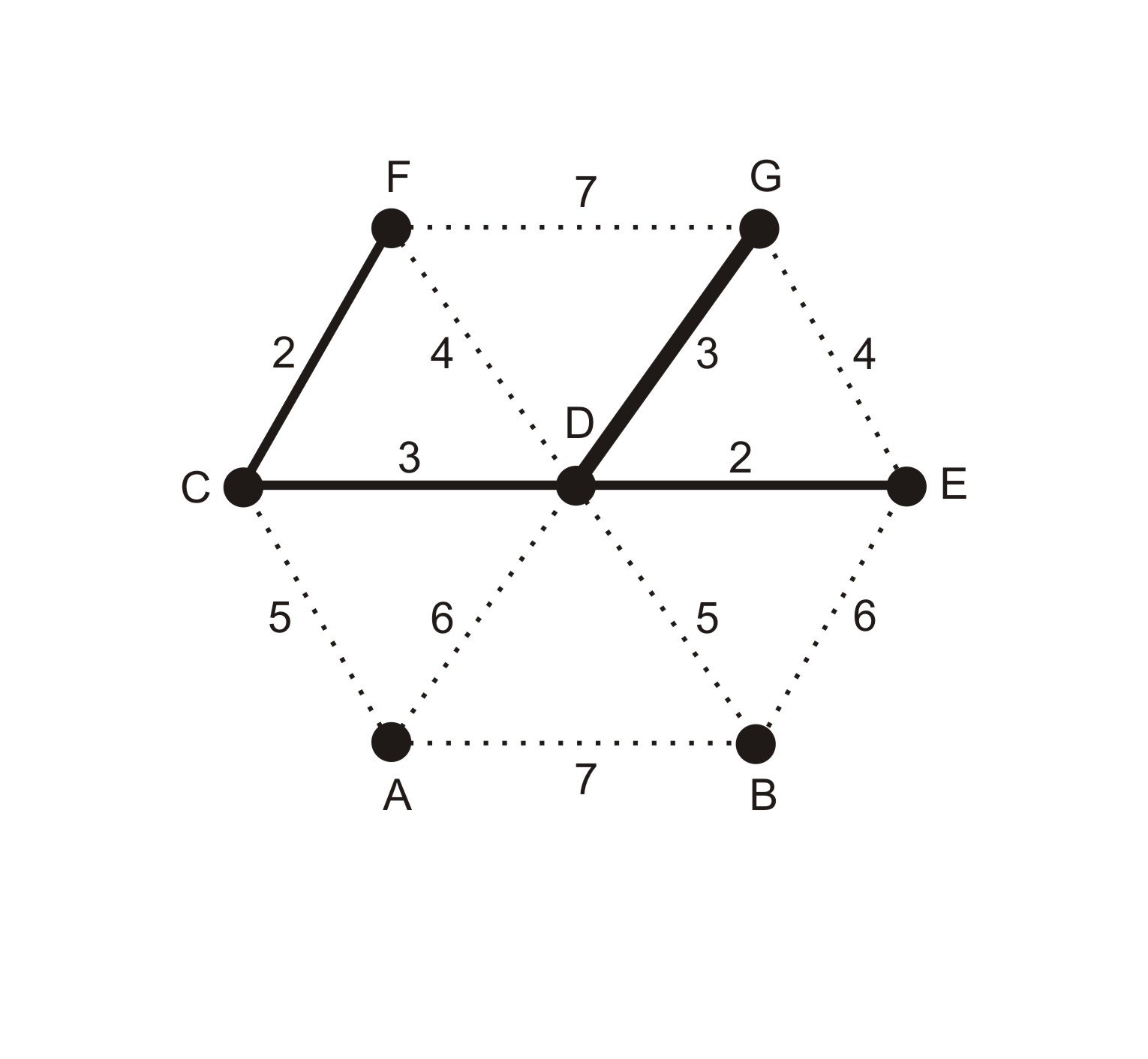
Při běžném provedení algoritmu pracujeme s vizuální reprezentací grafu. Hrany, které přidáváme do kostry, zvýrazňujeme (barevně či jiným způsobem) přímo v zadaném grafu. Na Obrázku 1 je znázorněn graf $H$ o sedmi vrcholech. Je ukázána situace před zpracováním 4. hrany v pořadí, mezi uzly $D$, $G$. Po prvních třech krocích se do kostry grafu vložily hrany $CF$, $DE$, $CD$. Jelikož přidáním hrany $DG$ nevytvoříme kružnici, můžeme ji taktéž vložit do kostry.
Příklad 1: Vážený neorientovaný graf $H$
V dalším pokračování však do kostry grafu nemůžeme přidat ani jednu hranu s ohodnocením 4, protože jejich vložením by v obou případech vznikla kružnice délky 3 (mezi trojicí $C, D, F$ či $D, E, G$).
Pro názornost uvádíme i konkrétní příklad váženého neorientovaného grafu a Animaci 1 naznačující výpočet minimální kostry pomocí Kruskalova algoritmu.
2. Návrh možných adaptací
1. Organizace hran grafu v tabulce podle vrcholů, zápis kostry do dalšího dokumentu (listu):
Graf je nabízen ve formě tabulky. Do jejího prvního sloupce zapisujeme návěští vrcholů. Do dalších buněk na stejném řádku pro daný vrchol $X$ vkládáme všechny hrany vycházející z $X$, a to ve formátu $X$–$n$–$Y$, kde $n$ je ohodnocení hrany a $Y$ je koncový vrchol hrany. $V$ dalším listu tabulky, případně v samostatném souboru, uchováváme hrany, které zařazujeme do minimální kostry. Taktéž tam evidujeme množiny uzlů, které jsou přidanými hranami propojeny. Uvažujme tentýž graf $H$ o sedmi uzlech, který jsme znázornili na Obrázku 1. Následující dvě tabulky (Tabulka 1 a Tabulka 2) zachycují stav po přidání prvních dvou hran do minimální kostry grafu $H$.
Příklad 3: Graf $H$ z Obrázku 1 po přidání dvou hran
| $A$ | $A$–$5$–$C$ | $A$–$6$–$D$ | $A$–$7$–$B$ | |||
| $B$ | $B$–$5$–$D$ | $B$–$6$–$E$ | $B$–$7$–$A$ | |||
| $C$ | $C$–$3$–$D$ | $C$–$5$–$A$ | ||||
| $D$ | $D$–$3$–$C$ | $D$–$3$–$G$ | $D$–$4$–$F$ | $D$–$5$–$B$ | $D$–$6$–$A$ | |
| $E$ | $E$–$4$–$G$ | $E$–$6$–$B$ | ||||
| $F$ | $F$–$4$–$D$ | $F$–$7$–$G$ | ||||
| $G$ | $G$–$3$–$D$ | $G$–$4$–$E$ | $G$–$7$–$F$ |
Příklad 4: Kostra grafu $H$ z Obrázku 1 po přidání dvou hran
Z předchozích dvou tabulek je patrné, že obě dosud přidané hrany propojují množiny uzlů $ \{ C, F\}$ a $ \{ D, E\}$. Před přidáním další hrany v pořadí $(C$–$3$–$D)$ musíme ověřit, zda v kostře grafu $H$ nevznikne kružnice. Vidomý student provádí kontrolu vizuálně, nevidomý si k tomuto účelu eviduje množiny uzlů propojených hranami dosavadní kostry. Pokud oba vrcholy zpracovávané hrany patří do stejné množiny uzlů, jejím přidáním bychom vytvořili kružnici. $V$ opačném případě aktualizujeme Tabulku 3. Aktuální hranu vkládáme do kostry a následně upravíme množiny vzájemně propojených uzlů. Nesmíme zapomenout, že právě zpracovaná hrana byla v Tabulce 2 uvedena dvakrát, je tudíž nutné oba výskyty vymazat.
2. Organizace hran ve dvou sloupcích tabulky, zápis kostry do dalšího dokumentu (listu):
Graf je opět nabízen ve formě tabulky, hrany jsou však organizovány jiným způsobem. V 1. sloupci je jejich charakteristika, opět ve formátu $x$–$n$–$y$, kde $x, y$ označují uzly propojené hranou s ohodnocením $n$. Ve 2. sloupci je znovu zopakováno ohodnocení hrany. Ukázku tohoto způsobu organizace hran nabízíme v Tabulce 3 .
Příklad 5: Hrany grafu $H$ z Obrázku 1 včetně ohodnocení
| $A$–$5$–$C$ | $5$ |
| $A$–$6$–$D$ | $6$ |
| $A$–$7$–$B$ | $7$ |
| $B$–$5$–$D$ | $5$ |
| $B$–$6$–$E$ | $6$ |
| $C$–$2$–$F$ | $2$ |
| $C$–$3$–$D$ | $3$ |
| $D$–$2$–$E$ | $2$ |
| $D$–$3$–$G$ | $3$ |
| $D$–$4$–$F$ | $4$ |
| $E$–$4$–$G$ | $4$ |
| $F$–$7$–$G$ | $7$ |
Většina tabulkových procesorů nabízí možnost seřadit data podle hodnot určitého sloupce. Nevidomý student tedy může hrany seřadit vzestupně podle ohodnocení, když je uspořádá podle 2. sloupce. Pro zápis kostry grafu a množin dosud propojených uzlů používáme buď druhý list tabulky či samostatný dokument. Postupujeme stejným způsobem jako v předchozí metodě.
3. Diskuze nad výhodami a nevýhodami
Poznamenejme rovnou, že druhou adaptaci nevidomí studenti hodnotili shodně jako lepší. Měli pro to tři hlavní důvody:
- ihned našli hranu, kterou mají aktuálně zpracovat;
- strávili méně času přesunem kurzoru mezi řádky a sloupci tabulky;
- nemuseli každou zpracovanou hranu dvakrát mazat ze zadání grafu.
U první metody studenti obtížně hledali hranu s aktuálně nejmenším ohodnocením. Řešení může být následující. Hrany s nejmenším ohodnocením je možné vyhledat postupným zadáváním řetězců "–$1$–", "–$2$–", atd. Jeden ze studentů přišel s dalším nápadem, a to rezignovat na reprezentaci grafu formou tabulky a využít podobným způsobem běžný textový editor, v němž hrany pro daný uzel $x$ umístíme na samostatný řádek. Nevidomí studenti tak plně mohou využít užitečných klávesových zkratek pro práci s textem i možností brailleského řádku.