Adaptace Matematických ALGoritmů

Pro násobení dvou matic $A$, $B$ (v tomto pořadí) je nutné splnit následující podmínku: počet sloupců matice $A$ musí být stejný jako počet řádku matice $B$. Je-li tomu tak, zapíšeme obě matice $A$, $B$ vedle sebe a napravo ponecháme prostor pro třetí, výslednou matici $C = A \cdot B$. Pro výpočet hodnoty matice $C$ na i-tém řádku a j-tém sloupci sledujeme i-tý řádek matice $A$ a j-tý řádek matice $B$, jejichž dílčí hodnoty násobíme a tyto součiny posléze sčítáme dohromady. Výsledný součet zapisujeme jako hodnotu matice $C$ na i-tém řádku a j-tém sloupci.

Pro lepší představu uvádíme i Příklad 1, jak získat hodnotu výsledné matice na konkrétním řádku a sloupci.

1. Práce s braillským výtiskem:

Nevidomý student má obě matice $A$, $B$ vytištěné na braillském výtisku, a to buď vedle sebe nebo pod sebou. Výslednou matici $C = A \cdot B$ zapisuje prostřednictvím klávesnice počítače v textovém editoru či tabulkovém procesoru, viz ukázka na Obrázku 1.

Příklad 2: Násobení matic na brailleském výstupu

Obrázek 1: násobení matic – dvojí uspořádání vstupních matic na brailleském výtisku

2. Práce s maticemi v jednom digitálním souboru:

V něm jsou obě matice $A$, $B$ i výsledná matice $C = A \cdot B$. Student využívá buď běžný textový editor či tabulkový procesor, v němž jsou všechny tři matice zapsány v jednom listu, viz Obrázek 2.

Příklad 3: Násobení matic v tabulkovém procesoru

Obrázek 2: násobení matic – obě vstupní matice jsou vloženy na jeden list tabulkového procesoru, stejně tak i výsledná matice

3. Každá ze tří matic je uložena v samostatném souboru (listu):

Mezi maticemi $A$, $B$ výslednou maticí $C = A \cdot B$ se student přepíná pomocí klávesové zkratky Alt+Tab, pracuje-li s běžným textovým editorem, případně využívá kombinaci Ctrl+PgUp, Ctrl+PgDown, jsou-li matice v samostatných listech jednoho souboru tabulkového procesoru.

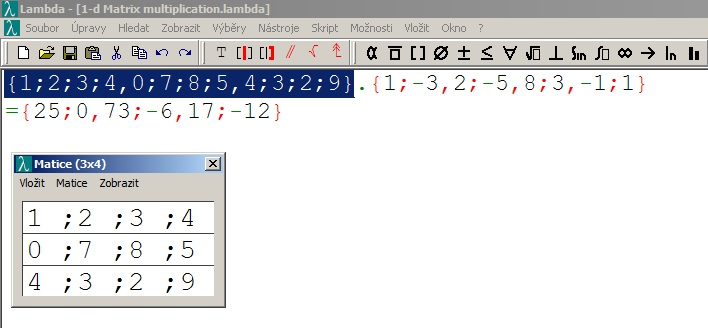
4. Práce s maticemi v editoru Lambda:

Jak již bylo zmíněno, editor Lambda má speciální nástroj pro práci s maticemi. Funguje podobně jako tabulkový procesor – nabízí možnost rychlého přepínání mezi maticemi pomocí klávesových zkratek PgUp a PgDown. Nevidomý student může do jednotlivých buněk vkládat i složitější výrazy, přitom má zajištěno, že budou narozdíl od běžných textových či tabulkových editorů korektně vysloveny odečítačem obrazovky či zobrazeny na braillském řádku. Ukázka viz Obrázek 3.

Příklad 4: Násobení matic v editoru Lambda

Obrázek 3: násobení matic v editoru Lambda

Shrneme nyní výhody a nevýhody všech čtyř metod adaptace algoritmu pro násobení dvou matic.

První metoda je výhodná především pro studenty, kteří s maticemi začínají pracovat. Potvrzuje to i nevidomý účastník workshopu: "Myslím, že pro začátek je vhodné používat pro demontraci matic a operací s nimi braillský výtisk, protože to zlepšuje představu o uspořádání hodnot v maticích."

Diskutovali jsme také otázku, zda je nevidomý člověk schopen číst informace v tištěném braillu na více pozicích současně? Případně, zda mu vyhovuje uspořádání matic vedle sebe či pod sebou. Účastníci nám potvrdili, že s tím nemají problém. Dokonce nepovažují za podstatné, zda jsou obě matice vedle sebe či pod sebou. Spíše jeden z nich potvrdil následující fakt: "Mám za to, že pokud budou hodnoty v matici komplexnější, pak již nebude možné se orientovat po sloupcích, protože hodnoty budou mít různý počet symbolů, tudíž nepůjdou seřadit vedle sebe."

Shodují se tedy v tom, že při seznámení s maticemi je výhodné je mít zobrazené v tištěné braillské podobě – nevidomý student si lépe představí strukturu matic a rozvržení hodnot po řádcích a sloupcích. Pro pokročilejší práci s maticemi obsahujícími komplexnější hodnoty je již nutné využít editor Lambda nebo tabulkový procesor.

Účastníci však potvrdili naši domněnku související s dosažitelností objektů, se kterými v průběhu výpočtu pracujeme. Práce se všemi třemi maticemi v jednom digitálním souboru (tedy druhá metoda) je příliš zdlouhavá a neefektivní. Člověk stráví spoustu času pohybem mezi oběma vstupními maticemi $A$, $B$, při hledání konkrétní buňky musí vždy přečíst všechny hodnoty v předcházejících řádcích či sloupcích. Chce-li být rychlejší, může si zapamatovat všechny hodnoty konkrétního řádku první matice, které postupně násobí s čísly či výrazy určitého sloupce druhé matice, a současně provádí součet těchto mezivýsledků. Je tedy více než jasné, že tento postup šetřící čas je prozměnu paměťově velmi náročný, a tím pádem náchylný k chybám.

Pracuje-li tedy nevidomý student s hodnotami všech tří matic na počítači, je pro něj optimální třetí či čtvrtá metoda. Výrazně se tím zlepšuje dosažitelnost konkrétního řádku či sloupce dané matice. Navíc, kurzor zůstává pro každou matici na místě, kde s ní nevidomý student pracoval naposledy, než se přepnul do jiného souboru či listu. Není tak nucen hledat konkrétní řádek či sloupec znovu.

Diskutovala se i otázka, zda je rozdíl mezi

1. uložením všech matic do tří samostatných souborů či
2. využitím jediného dokumentu a jeho tří listů.

Účastníci oba přístupy nerozlišují, takže sami považují první variantu za zbytečnou.

Ocenili též nástroj pro práci s maticemi, který nabízí editor Lambda. Výrazy v maticích obsahující složitější matematickou symboliku (mocniny a odmocniny, zlomky, písmena řecké abecedy aj.) jsou korektně reprodukovány nevidomému, ať už pomocí odečítače obrazovky či braillského řádku. Běžné tabulkové procesory takovou možnost nenabízí a pro vkládání speciálních matematických symbolů musí student vymyslet vlastní značky, pomocí nichž výrazy v maticích zapíše.

Posledním podnětem účastníků byla následující myšlenka: "Dle mého názoru by bylo užitečné, kdyby nevidomý čtenář mohl požádat aplikaci o přečtení jedné konkrétní buňky, nebo jednoho konkrétního řádku či sloupce matice, aniž by si nechat číst všechny předcházející hodnoty." Je to logický požadavek. Pokud např. student hodlá prozkoumat všechny hodnoty ve 4. sloupci matice $B$, musí nejprve projít přes tři buňky 1. řádku, což mu prodlužuje přístup k informaci, kterou hledá. Takový nástroj však neexistuje v žádném tabulkovém procesoru, ani editoru Lambda.