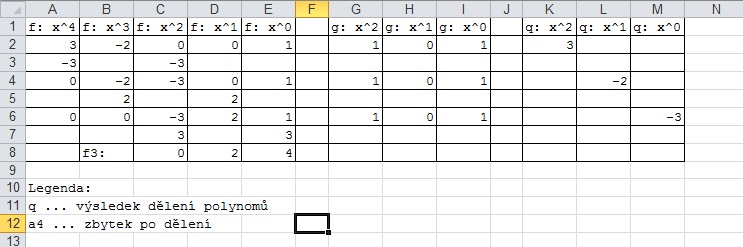
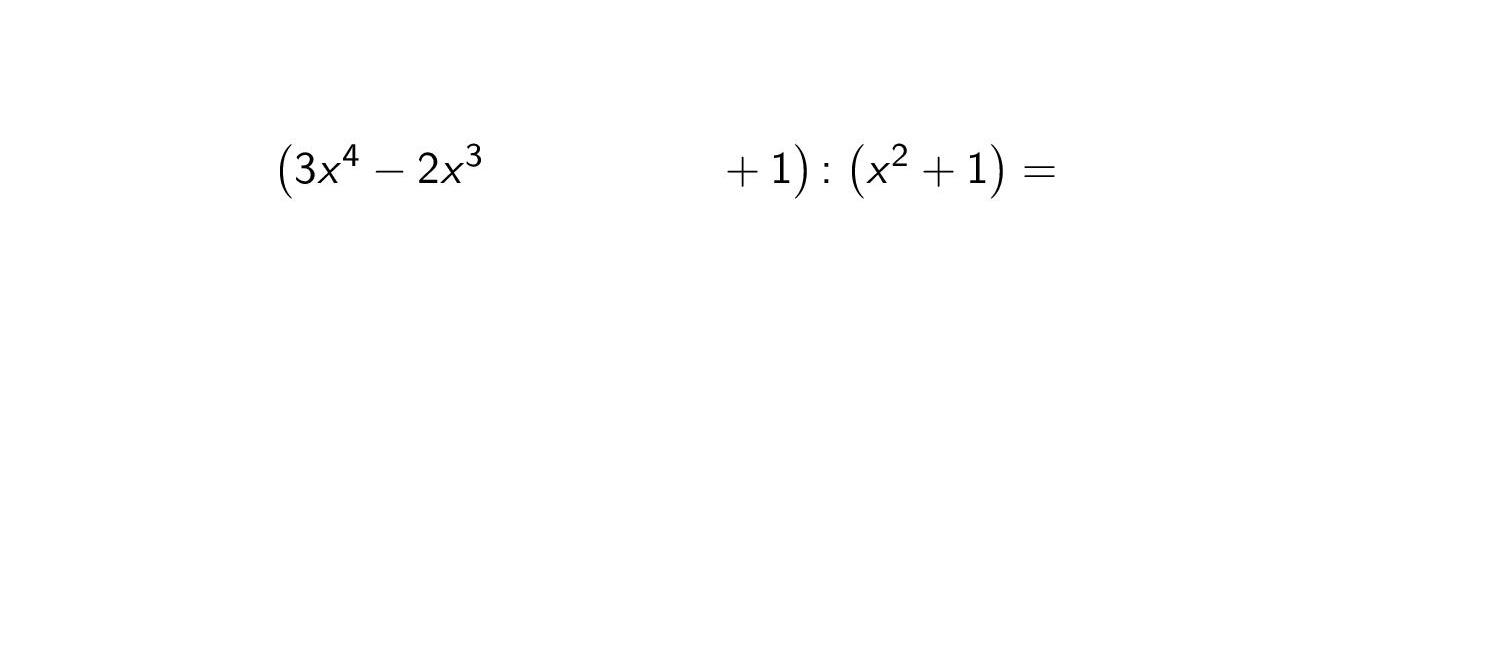Shrneme nyní výhody a nevýhody všech čtyř metod adaptace algoritmu dělení polynomu polynomem.
První metoda je výhodná, co se týče srozumitelnosti zapsaného výpočtu opravujícímu –
není třeba žádného dalšího vysvětlení. Bohužel je poměrně neúsporná, nevidomý student je nucen
vkládat vysvětlující text. Další nevýhodou je zdlouhavost výpočtu, případně paměťové nároky –
student si buď musí zapamatovat dělitele nebo jej musí pokaždé vyhledat v předcházejícím textu,
což jej značně zpomalí. I při závěrečném stanovení výsledku dělení je nucen
projít znovu celým výpočtem a "sesbírat" jednotlivé členy qá1š, qá2š, \dots, qánš.
Druhá metoda respektuje rovinné uspořádání polynomů dodržované při standardním provedení algoritmu
vidící osobou. Postup výpočtu je tak srozumitelný opravujícímu, i když jej může zpočátku mást fakt,
že se pracuje pouze s koeficienty členů jednotlivých polynomů. Účastníci
workshopu na ICCHP Summer University 2012 v Linci však připomněli i několik nevýhod:
-
Dosažitelnost jednotlivých koeficientů není snadná – nevidomý
student se poměrně zdlouhavě pohybuje mezi třemi objekty a nemá možnost ignorovat konkrétní hodnoty polynomů.
-
V tabulce se navíc těžko orientuje a často musí ověřovat, s jakou mocninou je daný koeficient spojen.
-
Chce-li ušetřit čas, tak je neustále zaměstnán udržováním mezivýsledků ve své paměti při
současném hledání pozice, na kterou je může vložit.
Možné řešení problému popsaném v bodě 2 navrhl jeden z nevidomých
účastníků workshopu:
"Pokud by si nevidomý uživatel mohl u libovolné buňky s koeficientem
přečíst mocninu umístěnou ve stejném sloupci, avšak v 1. řádku,
výrazně by to usnadnilo orientaci v tabulce. Stačilo by za tím účelem přidat skript či makro,
které by nahradilo zdlouhavý přesun na 1. řádek a zpět pomocí kurzorových šipek.
Analogickou adaptaci nabízí prof. José Enrique Fernández del Campo.
Jeho návrh zjednodušuje naši druhou metodu v tom, že se nevidomý student pohybuje pouze
mezi dvěma skupinami koeficientů. Prof. del Campo vychází z toho,
že dělitel se v průběhu výpočtu nemění, takže pod něj může postupně umisťovat i členy
(nikoli pouze koeficienty) výsledného podílu. Tím se částečně řeší 1. problém.
Sledujeme pouze dvě skupiny koeficientů (dělence a dělitele), přičemž členy výsledného podílu
zapisujeme pod dělitele. Dosažitelnost objektů, se kterými v algoritmu pracujeme, je
tím pádem snadnější. Nabízíme ukázku adaptace v editoru Lambda, v němž je pro zápis polynomů vhodně
použita funkce pro editaci matic, viz Obrázek 3.
Příklad 5: Dělení polynomů podle návrhu prof. del Campa
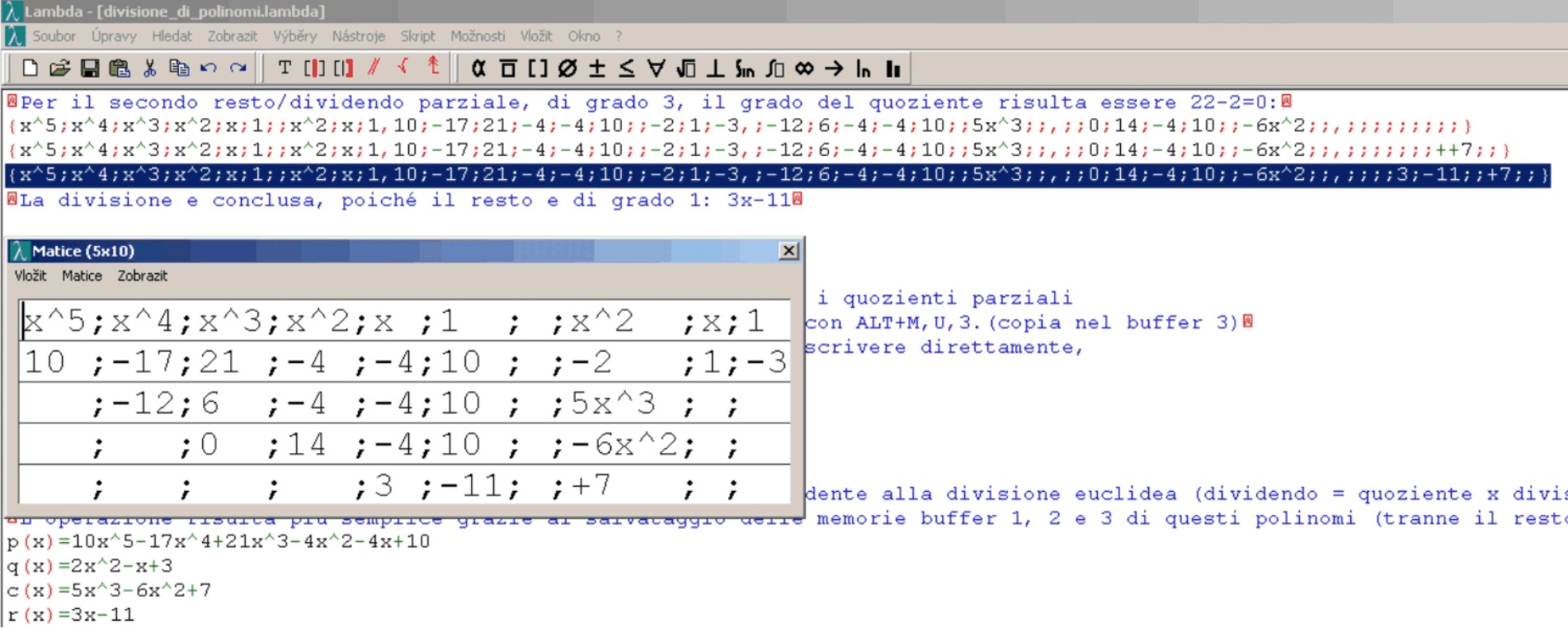 Obrázek 3:
dělení polynomů v Lambdě dle návrhu prof. del Campa
Obrázek 3:
dělení polynomů v Lambdě dle návrhu prof. del Campa
Zmiňme ještě článek Cristiana Bernareggiho s názvem
"Non-sequential Mathematical Notations in the LAMBDA System",
ve kterém se zabývá i adaptací algoritmu pro dělení polynomů. Jeho
přístup je v podstatě totožný s návrhem prof. del Campo, liší
se pouze v tom, že zápis polynomu pomocí koeficientů používá pouze v případě dělence
a polynomů fá1š, fá2š, \dots, fánš, fán +1š,
které zapisuje pod sebe.
Třetí metoda byla účastníky workshopu hodnocena nejpříznivěji. Její
nespornou výhodou je optimální dosažitelnost objektů, se kterými
aktuálně pracujeme. V každém kroku výpočtu provádíme určitou operaci
se dvěma polynomy a její výsledek zapisujeme na předem dané místo.
Proto je výhodné, když je máme co nejblíž. Nevidomý student si nejdříve vytvoří
prázdný řádek pro zapsání výsledku operace a následně se mezi oběma polynomy
pohybuje stiskem jediné klávesy. Snadno a bez paměťových nároků provede zadanou
operaci a její výsledek vloží nad nebo pod právě zpracovávané polynomy, čímž si
zajistí snadnou dosažitelnost objektů i pro následující kroky. Zápis výpočtu není
ihned srozumitelný opravujícímu, protože nerespektuje standardní umístění objektů, se kterými se
v algoritmu pracuje. Pokud však student veškeré polynomy zapisuje včetně jejich
pojmenování, postačí krátké vysvětlení v úvodu výpočtu.
Konečně čtvrtá metoda skýtá podobnou výhodu jak ta třetí,
a to snadnou dosažitelnost objektů polynomů, se kterými aktuálně pracujeme.
Není však příliš použitelná, chce-li nevidomý student prezentovat postup výpočtu opravujícímu.
Veškeré polynomy jsou rozděleny do tří souborů (resp. listů), učitel provádějící kontrolu
je tak nucen se mezi nimi neustále přepínat, což není pro vidící osobu příliš přívětivé.
Je proto žádoucí, aby student sám pomohl učiteli tím, že po ukončení výpočtu zkopíruje obsah
všech tří souborů (resp. listů) do jediného dokumentu.