Dijkstrův algoritmus
1. Popis standardní metody algoritmu
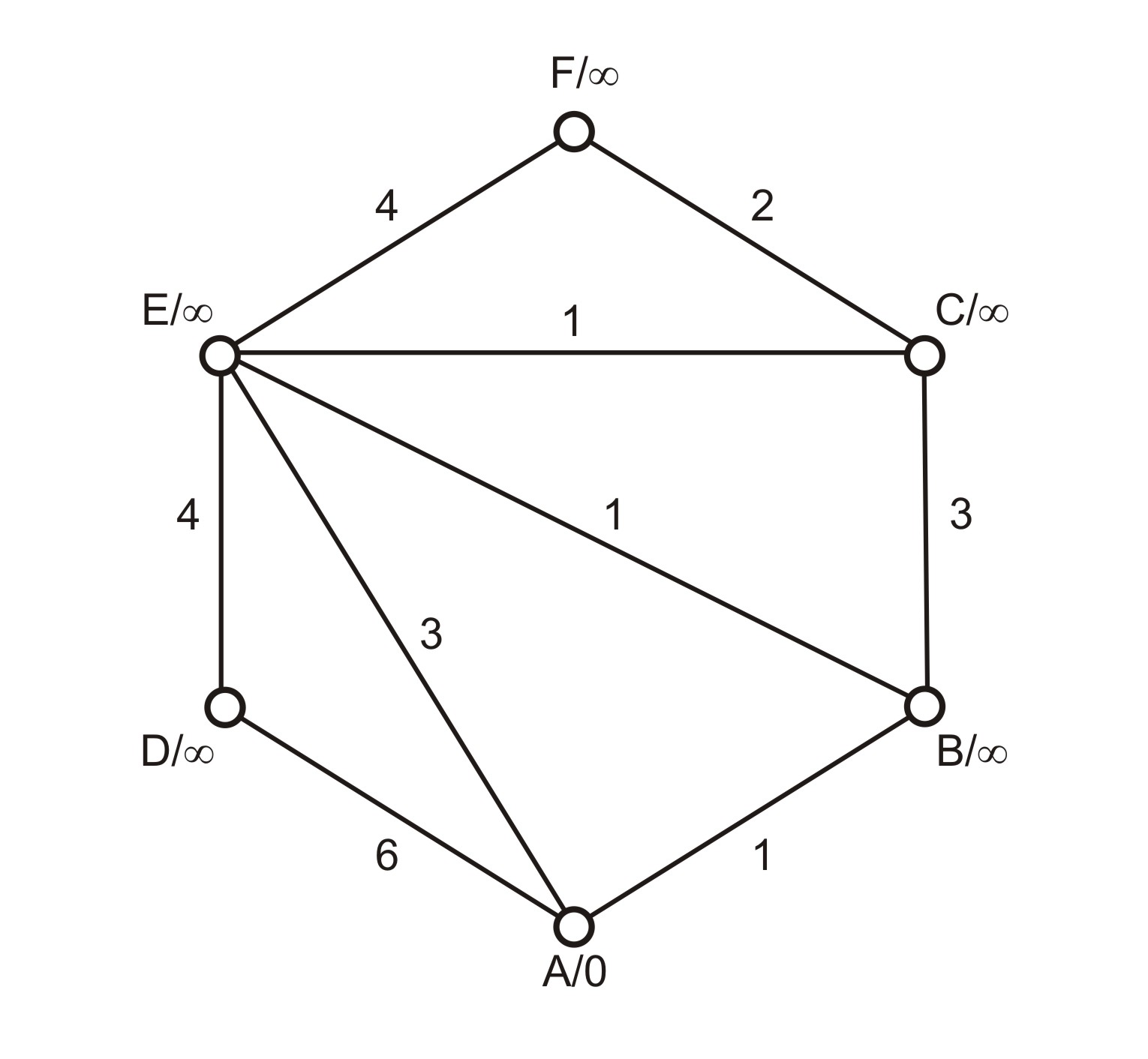
Dijkstrův algoritmus slouží k vyhledání nejkratší cesty z iniciálního uzlu A do všech ostatních uzlů grafu. Pracujeme s váženým neorientovaným grafem G = (V, E, w), kde V je množina vrcholů, E je množina neorientovaných hran a w je ohodnocení hran. Na počátku algoritmu vložíme do návěští iniciálního uzlu A hodnotu "A/0", do návěští ostatních uzlů X, jejichž vzdálenost od A zatím neznáme, zapíšeme "X/\infty". Ukázku takového grafu nabízíme na Obrázku 1.
Příklad 1: Neorientovaný graf G
Opakovaně provádíme následující tři kroky, dokud nezpracujeme všechny vrcholy:
- Mezi nezpracovanými vrcholy najdeme uzel "X/n" s nejmenší vzdáleností n od iniciálního V.
- Pro každou hranu e vedoucí z uzlu "X/n"
do nezpracovaného vrcholu "Y/m" provedeme následující:
- je-li m > n + w(e), změníme aktuální vzdálenost uzlu Y od iniciálního uzlu na m = n + w(e),
- v opačném případě ponecháme návěští uzlu Y beze změny.
- Označíme uzel X jako zpracovaný.
Při aplikaci Dijkstrova algoritmu měníme pouze návěští vrcholů. Aktualizujeme jejich aktuální vzdálenost od iniciálního uzlu, nebo je označujeme za zpracované. Pro názornost uvádíme i konkrétní příklad neorientovaného grafu a Animaci 1 naznačující výpočet nejkratších vzdáleností od iniciálního uzlu pomocí Dijkstrova algoritmu.
Příklad 2: Neorientovaný graf G
-
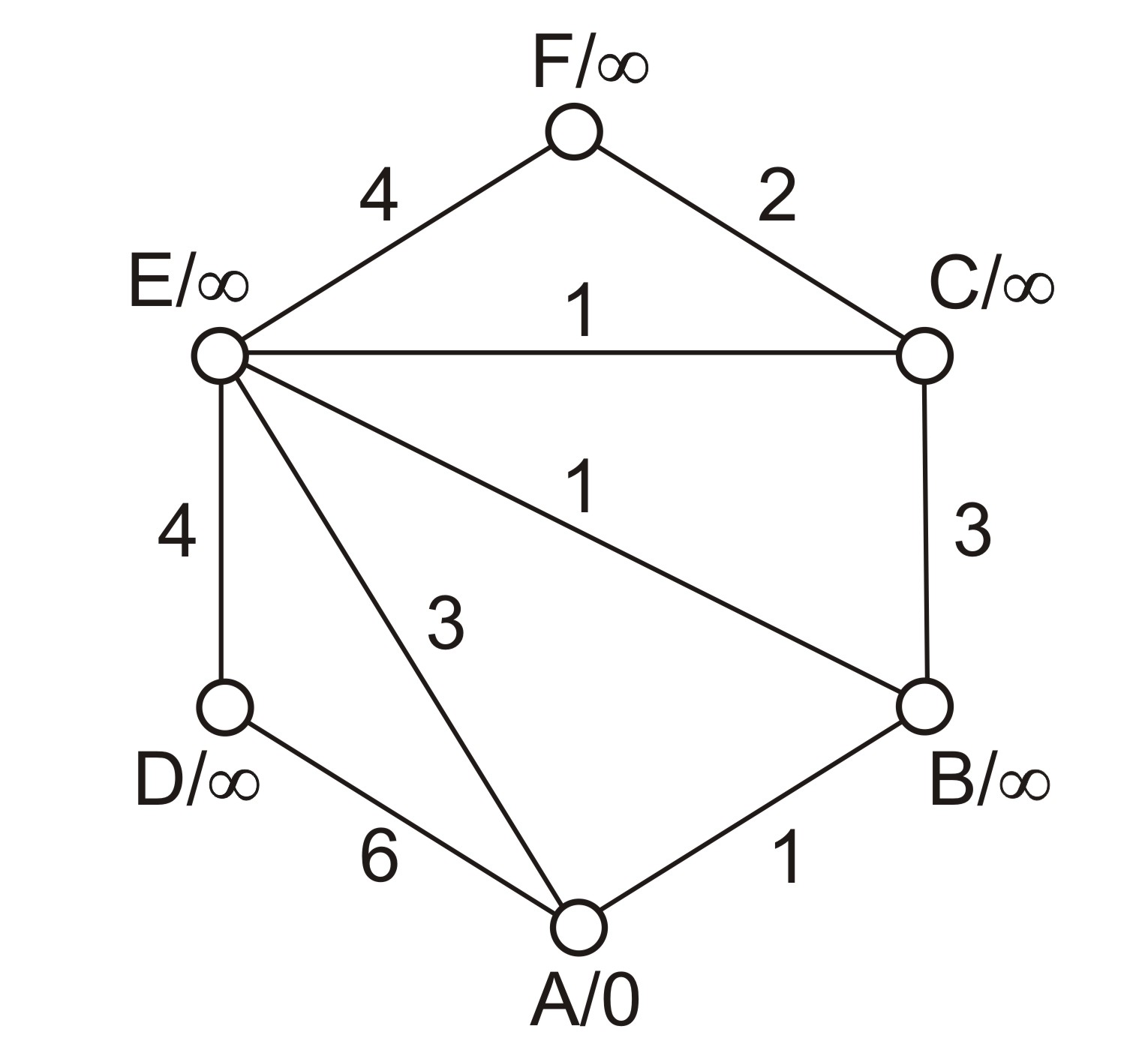
- Počátek algoritmu
A/0 B/ \infty C/ \infty D/ \infty E/ \infty F/ \infty - A/0 A–1–B A–6–D A–3–E
B/B–1–A B–3–C B–1–E
C/C–3–B C–1–E C–2–F
D/D–6–A D–4–E
E/E–3–A E–1–B E–1–C E–4–D E–4–F
F/F–2–C F–4–E
Nezobrazovat tento popisek