Ford-Fulkerson algorithm
1. Original procedure of the algorithm
Ford-Fulkerson algorithm is used to find the maximum flow in a flow network. We work with a network G = (V, E), where 0/1 is a set of nodes including a source S and sink T, E is a set of directed edges. A label of an edge is written as F/C where C indicates its capacity and F means a flow (amount of energy) streaming through the edge.
- At the beginning of the algorithm set the flow of all the edges to 0.
- We repeatedly search for the augmenting path from the source S to the sink T. As soon as we find such a path we also compute the available capacity of all its edges, by which we subsequently increase the flow in the network.
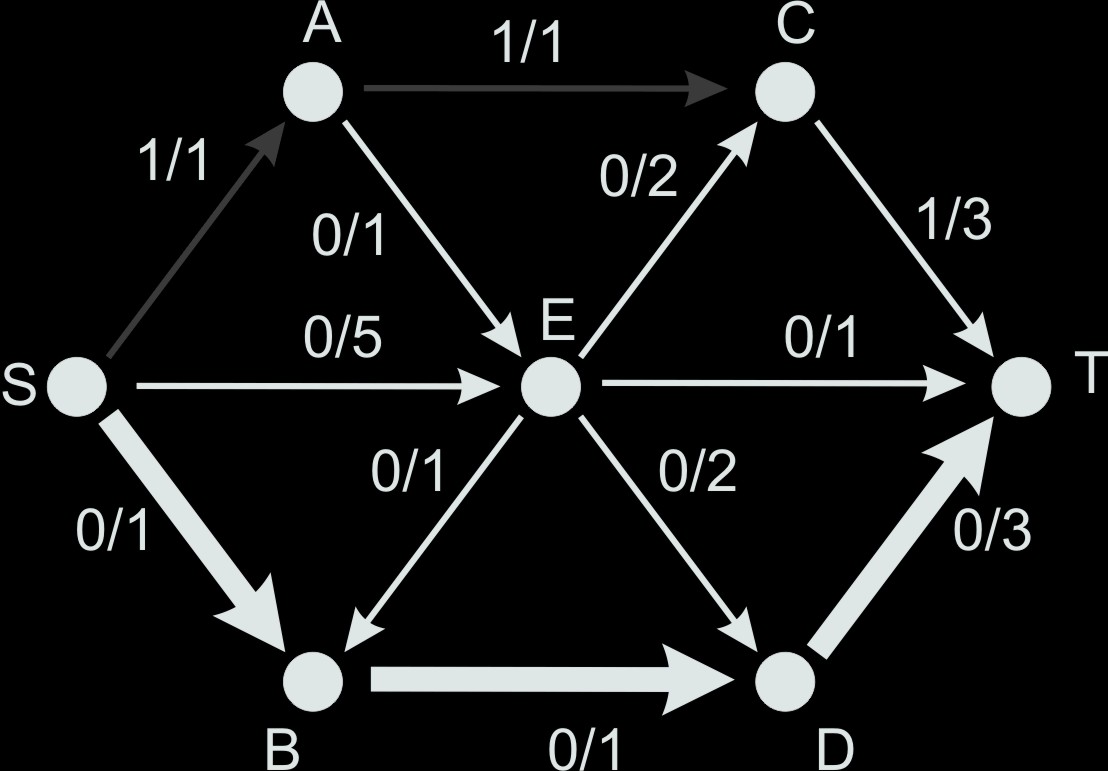
When processing the algorithm in the standard way we work with a visual representation of the network and modify labels of edges. Image 1 illustrates a network N with seven nodes and the current flow 1 (see the path S → A → C → T). The augmenting path S → B → D → T, with the available capacity 1 on all its edges is highlighted. In the next step we can increase the flow and modify labels of the augmenting path, change 0/1 to 1/1 for the paths S → B, B → D and 0/3 to 1/3 for the path D → T.
Example 1: network N
To demonstrate Ford-Fulkerson algorithm we come with an Animation 1 of the computation and use a concrete flow network.
Example 2: network N
-
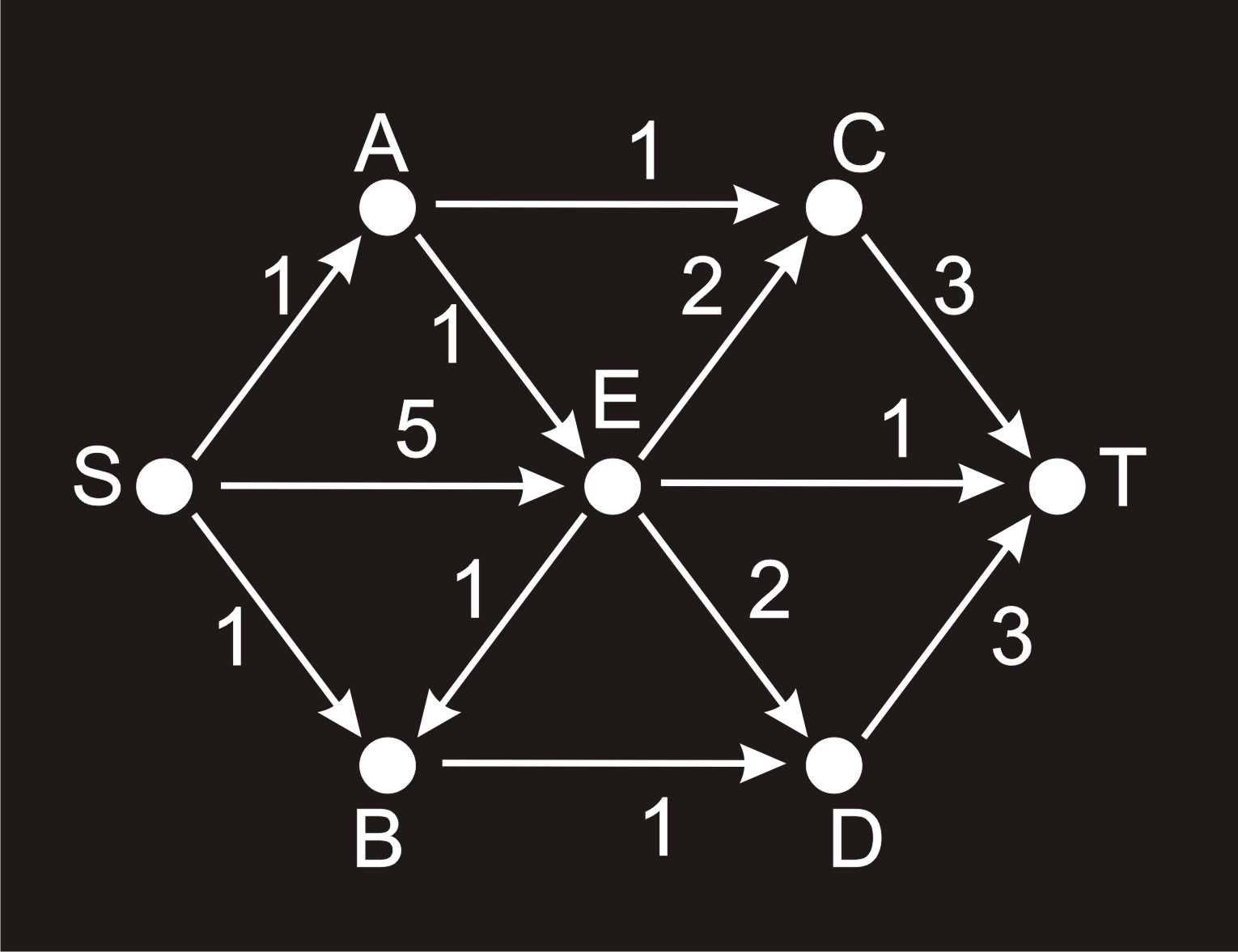
- Start of the algorithm – a flow network N with seven nodes S, A, B, C, D, E, T
- S: S–1–A S–1–B S–5–E
A: A–1–C A–1–E
B: B–1–D
C: C–3–T
D: D–3–T
E: E–1–B E–2–C E–2–D E–1–T
TDo not display this label