Analysis of the function graph
4. Sketching the graph of the function and its adaptation
The tradional last part of the function analysis is to sketch the graph. Students prove their comprehension to the meaning of all the data they counted before and how they are able to put these results together. Such a task is much more complicated for blind people. Three types of adaptions are considered:
- handmade production of the graph's tactile version using suitable assistive technology
- text description of the graph which helps a reader to imagine how it looks visually
- selection from several tactile images of graphs prepared in advance
We discussed pros and cons of all the three adaptions with participants of our workshop held during ICCHP Summer University 2012 in Linz. The handmade production of the function's tactile image is of course time consuming for blind people. They make much more effort than their sighted peers to ensure the result of their work to be corresponding with the reality.
We can confirm from our own experience the second method of adaptation is not very easy for a blind person. A long-term traning is needed to ensure the blind student is able to describe clearly the graph of the function whose properties he/she counted before. He/she often makes mistakes in ordering information when describing the graph. At first, he/she focuses on details and afterwards adds general information. To have a perfect picture of the graph in his/her mind the blind student needs to connect his/her description with a tactile image. One of the workshop's participants, a teacher of mathematics for blind confirmed that: "I think a blind student misses something if he only describes the graph and doesn't have its tactile version. The text description of the graph is not a hundred per cent replacement of its image."
It can be very easy to supervise the correctness of the graph's description.
The blind student provides a teacher or a classmate with the description and
asks him/her to sketch the graph without telling him/her the general form of the function.
If the drawing corresponds to the real image of the function, the blind student's
description is correct. We performed such a test with participants of
several workshops aimed at educational staff. We asked them to draw the graph
when having its text description (done by the blind student we have shown in
the previous part).
The result confirms the description is created well. All
the information are structured properly and teachers don't have problems to
understand it. We can share some interesting observations of teachers who
performed the test. They missed few details which we as the teachers of
the blind student had not noticed. For example, the description doesn't
contain the computation of the first derivative in the inflection point
which indicates how the function's graph changes at the neighborhood of
that point, how much it is close to the axis  .
.
There are several factors which affect the difficulty of the task when using the third method of adaptation. At first, the more tactile images are prepared the more time consuming it is to compare them and select the right one. Complexity of the task is also influenced by the number of details which distinguish one image from the other. If the difference is minor and hardly noticeable, the blind student has difficulties to choose the correct option. In our opinion the third method of adaption also tests different skills than in the case of sighted students. Having drawn the picture they prove to know how to put all the computed results together and to understand how they influence the graph. On the other side, the blind student pays attention only to differences between tactile images he receives. Having computed properties of the function he/she selects that one corresponding to the results of the previous work.

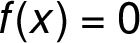 , describing intervals where the graph is above or below the axis
, describing intervals where the graph is above or below the axis 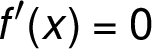 , determination of stationary points and intervals where the graph is increasing or decreasing.
, determination of stationary points and intervals where the graph is increasing or decreasing.
 , determination of inflection points and intervals where the graph concaves downward or upward.
, determination of inflection points and intervals where the graph concaves downward or upward.
 and the graph's analysis done by one of our blind students.
There's a key issue how to adapt the 7th task – sketching the graph after
computing all the necessary properties of the function. We will
focus on the problem in the part
and the graph's analysis done by one of our blind students.
There's a key issue how to adapt the 7th task – sketching the graph after
computing all the necessary properties of the function. We will
focus on the problem in the part  .
.

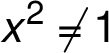
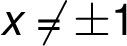

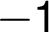 and
and 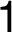 are the points of discontinuity.
are the points of discontinuity.








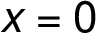

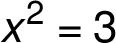




![[-\sqrt{ 3}, \frac{ -3\sqrt{ 3}}{ 2}] [-\sqrt{ 3}, \frac{ -3\sqrt{ 3}}{ 2}]](/amalg/www/images/latex/___lL__d__s_sqrt_L_3_R_,_s_frac_L__d_3_s_sqrt_L_3__norm14_.png)
![[\sqrt{ 3}, \frac{ 3\sqrt{ 3}}{ 2}] [\sqrt{ 3}, \frac{ 3\sqrt{ 3}}{ 2}]](/amalg/www/images/latex/___lL__s_sqrt_L_3_R_,_s_frac_L_3_s_sqrt_L_3_R__R___norm14_.png)

![=\frac{ 2x *(x^2 -1) *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^4} =\frac{ 2x *(x^2 -1) *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^4}](/amalg/www/images/latex/___e__s_frac_L_2x_S__l_x_P_2_d_1_r__S__lL__l_2x_P__norm14_.png)
![=\frac{ 2x *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^3} =\frac{ 2x *[(2x^2 -3) *(x^2 -1) -2(x^4 -3x^2)]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL__l_2x_P_2_d_3_r__S__l_x_P__norm14_.png)
![=\frac{ 2x *[2x^4 -3x^2 -2x^2 +3 -2x^4 +6x^2]}{ (x^2 -1)^3} =\frac{ 2x *[2x^4 -3x^2 -2x^2 +3 -2x^4 +6x^2]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL_2x_P_4_d_3x_P_2_d_2x_P_2_p_norm14_.png)
![=\frac{ 2x *[x^2 +3]}{ (x^2 -1)^3} =\frac{ 2x *[x^2 +3]}{ (x^2 -1)^3}](/amalg/www/images/latex/___e__s_frac_L_2x_S__lL_x_P_2_p_3_rR__R__L__l_x_P__norm14_.png)


 :
:  , A
, A :
:  , V
, V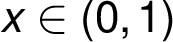 :
:  :
: ![[0, 0] [0, 0]](/amalg/www/images/latex/___lL_0,0_rR____norm14_.png) .
.
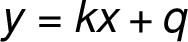 :
:

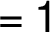


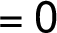
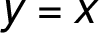 .
.
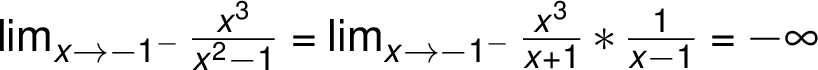



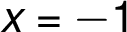 and
and 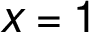 .
.
 .
The graph is limited by the vertical asymptotes
.
The graph is limited by the vertical asymptotes ![[-\sqrt{ 3}, -\sqrt{ 3}] [-\sqrt{ 3}, -\sqrt{ 3}]](/amalg/www/images/latex/___lL__d__s_sqrt_L_3_R_,_d__s_sqrt_L_3_R__rR____norm14_.png) lying on the asymptote
lying on the asymptote 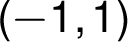 intersects with the axis
intersects with the axis  is located between the vertical asymptotes
is located between the vertical asymptotes ![[\sqrt{ 3}, \sqrt{ 3}] [\sqrt{ 3}, \sqrt{ 3}]](/amalg/www/images/latex/___lL__s_sqrt_L_3_R_,_s_sqrt_L_3_R__rR____norm14_.png) lying on the asymptote
lying on the asymptote