Matrix multiplication
1. Original procedure of the algorithm
To multiply two matrices $A, B$ (in the order as they are listed), it is necessary to meet the following requirement: the number of columns of the first matrix must be the same as the number of rows of the second matrix. If this condition is fulfilled, we usually write both matrices $A, B$ one beside the other and leave some space on the right for the third resulting matrix $C = A \cdot B$. Computing the value of the matrix $C$ in the row $i$ and the column $j$, we follow the row $i$ of the matrix $A$ and the column $j$ of the matrix $B$. We multiply relevant values and add these semi-results afterwards. The result of the addition is inserted into the given position of the matrix $C$.
We provide an Example 1 to make the algorithm more comprehensible:
2. Proposals of adaptation
1. Input matrices are printed in braille:
The blind student works with a tactile print where both matrices $A, B$ are written in braille, beside or above each other. He uses a text editor or spreadsheet to put down the values of the resulting matrix $C = A \cdot B$, see Image 1.
Example 2: Matrix multiplication on a braille print
2. All three matrices are inserted in one digital file:
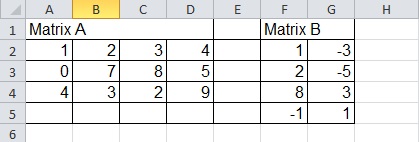
The blind student works with a standard text editor or spreadsheet in which the matrices are listed in one sheet, beside or below each other, see Image 2.
Example 3: Matrix multiplication in a spreadsheet
3. Each matrix is located in one separate file (or sheet):
The
blind student can switch between the files (or sheets of
a spreadsheet) by pressing the key combination Alt+Tab (or
Ctrl+PgUp, Ctrl+PgDown).
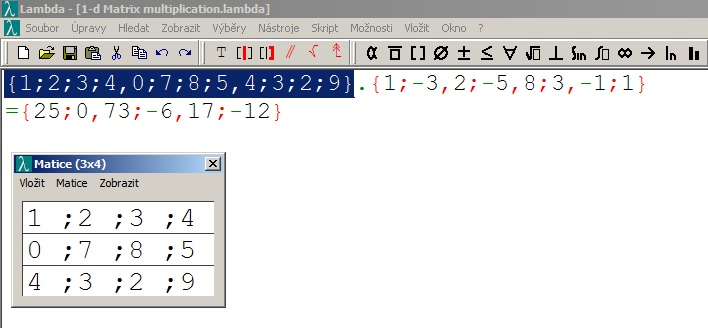
4. The matrices are processed in the Lamba editor:
As already mentioned, the Lambda editor provides users with
a special tool for manipulation with matrices which works in
a similar way as spreadsheets. The blind student can switch between
matrices very quickly by pressing the keys PgUp, PgDown.
Additionally he
can also insert complex expressions combined from powers, square roots,
fractions, Greek letters, etc., which, unlike standard text editors or
spreadsheets, are reproduced by a screenreader or
a refreshable braille display in the correct way according to the
authorized national 8-dot rules. See Image 3.
3. Discussion of pros and cons
We summarize the pros and cons of all the four methods of the matrix multiplication adaptation.
The first method is useful for students who begin working with matrices. One of the workshop participants confirmed that: "I think that the braille print is optimal to use during the introductory lessons about matrices. The teacher could demonstrate the basic properties of the matrix more easily. Thanks to the braille print a student has a better idea about the arrangement of values in the matrix."
We also discussed the question of whether a blind person is able to read information in the braille print located at different positions at the same time, and whether he/she prefers the matrices arranged one beside the other or one below the other. The workshop participants declared they did not have a problem with simultaneous reading of two sources of information at different positions. What is more, they do not distinguish between the two types of arrangement of matrices mentioned above. Rather, they confirmed the following fact: "If values of the matrix are complex, then they cannot be aligned vertically because of their different length; that’s why it is not possible to follow them in columns."
Therefore they all agree that it is suitable for blind students studying matrices for the first time to use a tactile print as it helps them imagine their structure and arrangement of values in rows and columns better. For those who work with complex values in matrices it is necessary to use the editor Lambda or a spreadsheet.
The workshop participants validated our assumption concerning the accessibility of objects we work with during the computation. Manipulation with three matrices in one digital file (the second method) is too time-consuming and inefficient. One spends a lot of time moving between both input matrices $A, B$ because he has to read through all the values in previous rows and columns. To speed up the computation he can remember the particular row’s values of the first matrix which he multiplies with numbers or expressions located in the given column of the second matrix. At the same time he/she adds up these semi-results. It is absolutely clear that although this approach saves time, it also causes overloading of memory and therefore it can lead to mistakes during the computation.
If blind students manipulate matrices only on a computer, the third of fourth method is optimal. They can access the particular row or column very easily. Additionally, when they leave the matrix located in the particular file (or sheet) and move to the other one, the cursor stays on the position where it was the last time. Therefore if they return to the matrix they do not have to look for the relevant row or column again.
There was a question whether the workshop participants distinguish between
- distributing all three matrices to separate files or
- using sheets of only one spreadsheet document.
They were not able to recognize any substantial difference between these two approaches, therefore they consider the first option as redundant.
They also appreciated the Lambda tool for matrix manipulation. Expressions including complicated mathematical symbols (powers and square roots, fractions, Greek letters, etc.) are correctly reproduced to the blind user whether by a screenreader or a refreshable braille display ()According to the relevant national 8-dot rules. Standard spreadsheets do not provide users with this kind of service.
Finally, the workshop participiants suggested the following idea. "It would be useful if the blind person could ask the application to read the content of one single cell, row, or column of the matrix without having to go through all the previous values". This is a reasonable requirement. For example, if the student intends to analyze the fourth column of matrix $B$, he/she has to pass first three cells of the first row, which slows down the process of looking for the information.